Nuestra vida está llena de incertidumbre. Muchas veces queremos conocer información que está fuera de nuestro alcance, por lo que tenemos que conformarnos con aproximaciones. El problema de las aproximaciones es que están sujetas a error, por lo que nunca podemos estar completamente seguros de que nuestras estimaciones sean ciertas. Eso sí, podemos medir nuestro grado de incertidumbre.De eso se encarga en gran parte la estadística, de cuantificar la incertidumbre. Por ejemplo, supongamos que queremos saber cuál es el valor medio de colesterol de los adultos de entre 18 y 65 años de la ciudad donde vivo. Si quiero el valor medio exacto tengo que llamarlos a todos, convencerlos para que se dejen hacer un análisis (la mayoría estarán sanos y no querrán hacerse nada) y hacer la determinación a cada uno de ellos para calcular después la media que quiero conocer.
El problema es que vivo en una ciudad muy grande, con unos cinco millones de habitantes, así que es imposible desde un punto de vista práctico determinar el colesterol a todos los adultos del intervalo de edad que me interesa. ¿Qué puedo hacer?. Tomar una muestra más asequible de mi población, calcular el valor medio de colesterol y estimar cuál es el valor medio de toda la población.
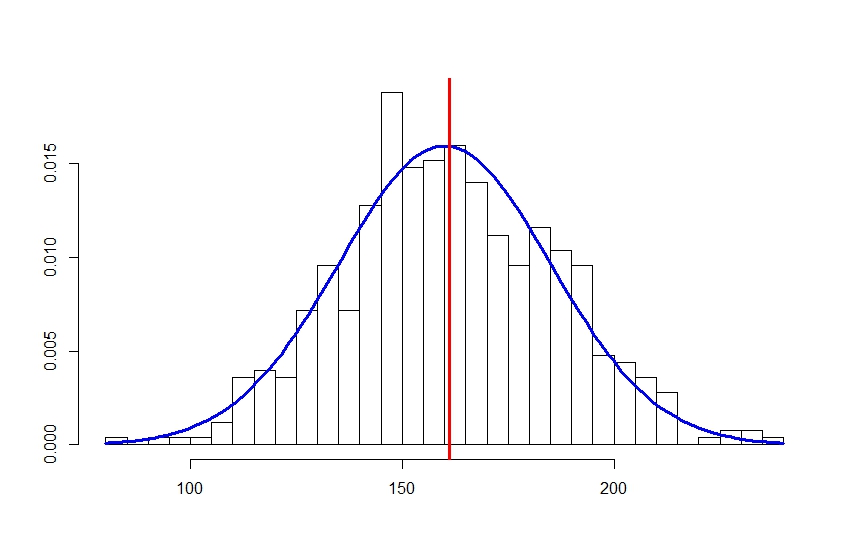
Así que escojo 500 individuos al azar y determino sus valores de colesterol en sangre, en miligramos por decilitro, obteniendo una media de 165, una desviación estándar de 25 y una distribución de los valores aparentemente normal, tal como os muestro en la figura que se adjunta.
Lógicamente, como la muestra es bastante grande, el valor medio de la población probablemente estará cerca de los 165 que he obtenido de la muestra, pero también es muy probable que no sea exactamente ese ¿Cómo puedo saber el valor de la población? La respuesta es que no puedo saber el valor exacto, pero sí aproximadamente entre qué valores está. En otras palabras, puedo calcular un intervalo dentro del cual se encuentre el valor inasequible de mi población, siempre con un nivel de confianza (o incertidumbre) determinado.
Pensemos por un momento qué pasaría si repitiésemos el experimento muchas veces. Cada vez obtendríamos un valor medio un poco diferente, pero todos ellos deberían ser parecidos y próximos al valor real de la población. Si repetimos el experimento cien veces y obtenemos cien valores medios, estos valores seguirán una distribución normal con un valor medio y una desviación estándar determinados.
Ahora bien, sabemos que, en una distribución normal, aproximadamente el 95% de la muestra se encuentra en el intervalo formado por la media más menos dos desviaciones estándar. En el caso de la distribución de medias de nuestros experimentos, la desviación estándar de la distribución de medias se denomina error estándar de la media, pero su significado es el mismo que el de cualquier desviación estándar: el intervalo comprendido por la media más menos dos errores estándar contiene el 95% de las medias. Esto quiere decir, aproximadamente, que la media de nuestra población se encontrará el 95% de las veces en el intervalo formado por la media de nuestro experimento (no necesitamos repetirlo cien veces) más menos dos veces el error estándar. ¿Y cómo se calcula el error estándar de la media?. Muy sencillo, aplicando la fórmula siguiente:
error estándar = desviación estándar / raíz cuadrada del tamaño de la muestra
En nuestro caso, el error estándar vale 1,12, lo que quiere decir que el valor medio de colesterol en nuestra población se encuentra dentro del intervalo 165 ““ 2,24 a 165 + 2,24 o, lo que es lo mismo, de 162,76 a 167,24, siempre con una probabilidad de error del 5% (un nivel de confianza del 95%).
Hemos calculado así el intervalo de confianza del 95% de nuestra media, que nos permite estimar entre qué valores se encuentra el valor real. Todos los intervalos de confianza se calculan de forma similar, variando en cada caso la forma de calcular el error estándar, que será diferente según se trate de una media, una proporción, un riesgo relativo, etc.
Para terminar esta entrada comentaros que la forma en la que hemos hecho este cálculo es una aproximación. Cuando conocemos la desviación estándar de la población podemos utilizar una distribución normal para el cálculo del intervalo de confianza. Si no la conocemos, que es lo habitual, y la muestra es grande, cometeremos poco error aproximando con una normal. Pero si la muestra es pequeña, la distribución de medias ya no sigue una normal, sino una t de Student, por lo que tendríamos que utilizar esta distribución para el cálculo del intervalo. Pero esa es otra historia…
Bibliografía
1.- Bowers D. Estimating the value of a single population parameter – the idea of confidence intervals. Medical statistics from scratch, 2nd ed. John Wiley & Sons ltd. West Sussex, England, 2008:111-8. (web)
Entrada publicada previamente en Ciencia Sin Seso… Locura Doble


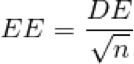


1 Comment