Manuel Molina Arias
Servicio de Gastroenterología Pediátrica
Hospital Universitario La Paz. Madrid
Suele decirse que las comparaciones son odiosas. Y la verdad es que no es muy conveniente comparar personas o cosas entre sí, ya que cada cual tiene sus valores y no tiene porqué sentirse menospreciado por ser o hacer algo de forma diferente. Así que no es de extrañar que el mismo Quijote dijese que las comparaciones son siempre odiosas. Claro que esto puede referirse a la vida cotidiana, porque en medicina nos pasamos el tiempo comparando unas cosas con otras, a veces de forma más que provechosa.
Hoy vamos a hablar de cómo comparar 2 distribuciones de datos de forma gráfica y vamos a fijarnos en una aplicación de este tipo de comparaciones que nos sirve para comprobar si nuestros datos siguen una distribución normal.
Imaginad por un momento que tenemos una serie de 100 valores de colesterol sérico de niños escolares ¿Qué pasaría si representásemos los valores frente a sí mismos de forma lineal? Sencillo: el resultado sería una línea recta perfecta que cruzaría la diagonal del gráfico.
Ahora pensemos que pasaría si en vez de compararla consigo misma la comparamos con otra distribución diferente. Si las 2 distribuciones de datos son muy parecidas, los puntos del gráfico se colocarán muy cerca de la diagonal. Si las distribuciones difieren, los puntos se irán lejos de la diagonal, tanto más lejos cuanto más diferentes sean las dos distribuciones. Veamos algún ejemplo.
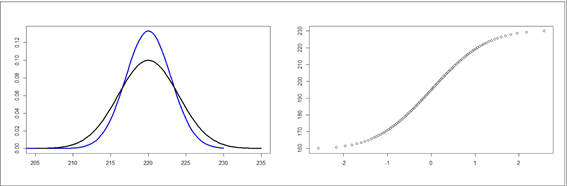
Supongamos que dividimos nuestra distribución en 2 partes, el colesterol de los niños y el de las niñas. Según nos dice nuestra imaginación, nuestros niños comen más bollería industrial que las niñas, así que sus valores de colesterol son mayores, como podéis comprobar si comparáis en la figura 1 la curva de las niñas (negro) con la de los niños (azul). Ahora, si representamos los valores de las niñas frente a los de los niños de forma lineal, tal como puede verse en gráfico, los valores se alejan de la diagonal, estando de manera uniforme por encima de ella ¿Esto a qué se debe? A que los valores de los niños son mayores y diferentes de los de las niñas.
Me diréis que todo esto está muy bien pero que puede resultar un poco innecesario. Total, si queremos saber cuáles tienen el valor más alto no tenemos más que mirar las curvas. Y tendréis razón en este caso, pero este tipo de gráficos se ha ideado para otra cosa, que no es otra que para comparar una distribución con su equivalente normal.
Imaginad que tenemos nuestra primera distribución y queremos saber si sigue una distribución normal. No tenemos más que calcular su media y su desviación estándar y representar sus quantiles frente a los quantiles de la distribución estándar teórica con la misma media y desviación. Si nuestra distribución es normal, los datos se alinearán cerca de la diagonal del gráfico. Cuanto más se alejen, menos probable será que nuestros datos sigan una distribución normal. Este tipo de gráfico se conoce como gráfico de quantil-quantil o, más comúnmente, por su nombre abreviado en inglés, q-q plot.
Veamos algún ejemplo de q-q plot para entenderlo mejor. En la figura 2 veis 2 curvas, una azul que representa una distribución normal y una negra que sigue una t de Student. A la derecha podéis ver el q-q plot de la distribución de la t de Student. Los datos de la parte central se ajustan bastante bien a la diagonal, pero los extremos lo hacen peor, variando la pendiente de la recta. Esto nos indica que hay más datos en las zonas de las colas de los que habría si la distribución fuese normal. Claro que esto no debería extrañarnos, ya que sabemos que las“ colas pobladas“ son una de las características de la distribución de Student.
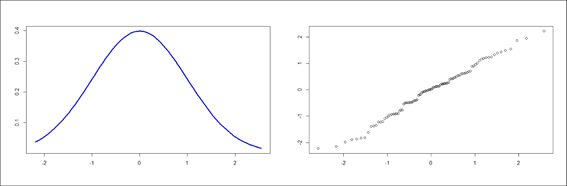
Por último, en la figura 3 veis una distribución normal y su q-q plot, en el que podemos ver cómo los datos se ajustan bastante bien a la diagonal del gráfico.
Veis, pues, como el q-q-plot es un método gráfico sencillo para determinar si una distribución de datos sigue una normal. Me diréis que puede resultar un poco latoso calcular los cuantiles de nuestra distribución y los de la normal para poder representar unos frente a otros, pero recordad que la mayor parte de los programas de estadística lo hacen sin esfuerzo. Sin ir más lejos, R tiene una función llamada qqnorm que dibuja el q-q plot en un parpadeo.
Y aquí vamos a dejar los ajustes a la normal por hoy. Recordaos que hay otros métodos más exactos de tipo numérico para saber si los datos se ajustan a la distribución normal, como la prueba de Kolmogorov-Smirnov o la de Shapiro-Wilk. Pero esa es otra historia…
Bibliografía
1.- Sí¼rí¼cí¼ B, Koí§ E. Assesing the validity of a statistical distribution: some illustrative examples from dermatological research. Clin Exp Dermatol.2008;33:239-42. (PubMed)