Ciencia sin seso… locura doble, una sección orientada a la metodología de la ciencia presentada por el Dr. Manuel Molina
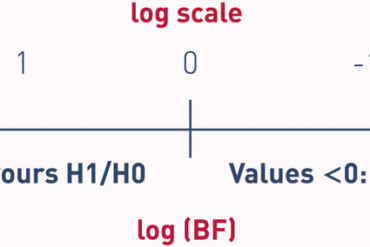
Se describen los conceptos de odds y probabilidad, así como su uso combinado junto al factor o regla de Bayes para los cálculos de la probabilidad de estar enfermo o sano tras conocer el resultado de una prueba diagnóstica.
Manuel Molina Arias.Servicio de Gastroenterología.Hospital Infantil Universitario La Paz.Madrid. España. La distribución normal no deja de sorprendernos por su belleza y armonía, a la…
La media geométrica se utiliza cuando los valores de la distribución de datos cambian de forma multiplicativa, y no aditiva. Esto la hace ideal para promediar datos de progresión geométrica, como razones, interés compuesto en economía o crecimientos de bacterias en microbiología.
Antes de utilizar una prueba de contraste paramétrica deberemos comprobar que la variable sigue una distribución normal. Para esta comprobación disponemos de tres estrategias posibles: los métodos basados en contrastes de hipótesis, los basados en representaciones gráficas y los llamados métodos analíticos.
El tamaño muestral necesario para estimar una media poblacional depende del nivel de confianza y precisión deseados, además la varianza de la variable en la población.
El tamaño muestral necesario para estimar una proporción poblacional depende del nivel de confianza y precisión deseados, además del valor de la proporción en la población.