Manuel Molina Arias.
Servicio de Gastroenterología.
Hospital Infantil Universitario La Paz.
Madrid. España.
Ya sabemos que la distribución normal es una de las más utilizadas en biomedicina, ya que un gran número de variables aleatorias siguen esta distribución. Aunque la función de densidad de esta distribución de probabilidad es bastante antipática, lo suple con el hecho de que se pueda caracterizar la distribución con solo dos parámetros, la media y la varianza, con lo que podemos realizar múltiples cálculos de probabilidad.
Vamos a realizar unos ejemplos de estos cálculos, utilizando para ello el programa R y ayudándonos de su interfaz gráfica R-Commander. Aunque R tiene las ventajas de ser muy potente y totalmente gratuito, su uso exclusivo desde la línea de comandos puede ser un poco duro para los no iniciados.
Unos preparativos previos
Como es lógico, para realizar cálculos sobre un conjunto de datos, lo primero que vamos a necesitar es ese conjunto de datos.
En la vida real ya los tendríamos. Serían los resultados de nuestro estudio los que llevaríamos a R para hacer el estudio estadístico.
En esta ocasión, nos vamos a fabricar los datos generando una distribución aleatoria con R.
Hay que decir, en primer lugar, que los programas estadísticos no generan números aleatorios, sino pseudoaleatorios, realizando cálculos a partir de un número previo que se suele denominar con el nombre de semilla.
En la práctica no nos importa, sirven igual para lo que queremos. El problema es que la semilla puede ser diferente en cada instalación de R, así que, si queréis seguir los ejemplos de esta entrada, lo primero es que todos establezcamos la misma semilla.
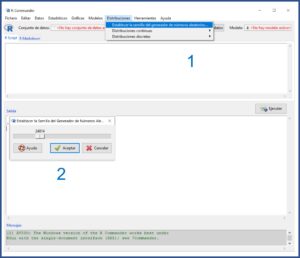
Primero lanzamos R. Segundo, lanzamos R-Commander con el comando library(Rcmdr). Tercero, seleccionamos la opción del menú Distribuciones -> Establecer la semilla del generador de números aleatorios. En la ventana emergente que aparece seleccionamos, por ejemplo, el 24814. Podéis verlo en la figura 1. Esto puede hacerse también con el comando set.seed(24814).
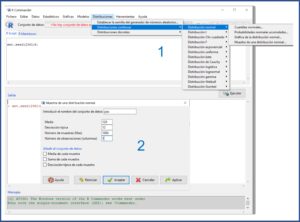
Generemos ahora los datos. Vamos de nuevo al menú Distribuciones, pero esta vez seleccionamos Distribuciones continuas->Distribución normal->Muestra de una distribución normal. Vamos a generar una muestra de 1000 casos con una media de 120, una desviación estándar de 12 y, obviamente, distribuida de forma normal. Para ello, rellenamos la ventana emergente tal como se muestra en la figura 2. Fijaos que, en el nombre del conjunto de datos, introducimos “pas”.
Ya lo tenemos todo. ¡A trabajar!
Paso 1. Comprobar la normalidad de los datos
Ya tenemos nuestra base de datos, llamada “pas”, que vamos a suponer es un registro de la presión arterial sistólica de 1000 adolescentes.
No vamos a entrar aquí en cómo hacer el estudio estadístico descriptivo básico. Haremos solamente un mínimo resumen numérico para comprobar que los datos están bien. Abrimos el menú Estadísticos->Resúmenes->Resúmenes numéricos.
Vemos que nuestros registros tienen una media de 119,78 (nos quedamos con 120) y una desviación estándar de 11,83 (nos quedamos con 12). El programa nos proporciona también la mediana, los cuartiles, el rango intercuartílico y el tamaño de la muestra.
Vamos a comprobar que siguen una distribución normal. Abrimos el menú Estadísticos->Resúmenes->Test de normalidad… En la ventana emergente marcamos, por ejemplo, la prueba de Shapiro-Wilk. Cuando aceptamos, el programa nos da un estadístico W=0,99 con un valor de p=0,58.
Como p > 0,05, no podemos rechazar la hipótesis nula que, para esta prueba, asume que los datos son normales. Pero ya sabemos que estas pruebas numéricas son poco potentes, así que conviene complementar este resultado con algún método gráfico.
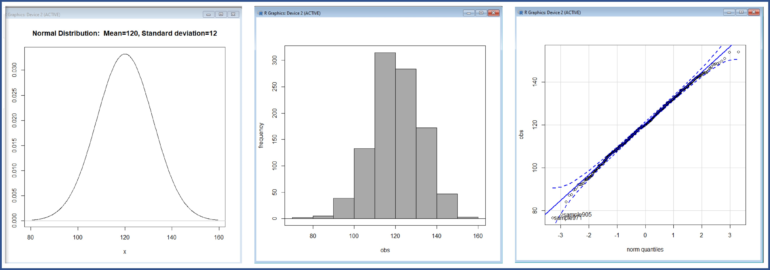
Seleccionamos Distribuciones-> Distribuciones continuas->Distribución normal->Gráfica de la distribución normal…, Gráficas->Histograma, y Gráficas->Gráfica de comparación de cuantiles… Obtenemos así la representación gráfica de la distribución, su histograma y el gráfico de cuantiles teóricos, respectivamente, que podéis ver en le figura 3.
Tanto la representación gráfica de la curva, como la forma del histograma, son compatibles con una distribución normal. Además, en el tercer gráfico, los puntos siguen bastante bien la diagonal, lo que significa que los cuantiles de la distribución se asemejan bastante bien a los teóricos si la distribución fuese normal.
En resumen, podemos asumir que nuestros datos siguen una distribución normal.
Paso 2. Información directa que obtenemos de la distribución
Sabiendo que la presión arterial de nuestros adolescentes sigue una distribución normal de media m=120 y desviación estándar s=12, podemos ya sacar una serie de conclusiones.
En una distribución normal, los valores se agrupan de forma simétrica en torno a la media. El 68% de la población se agrupa alrededor de la m ± 1 s, el 95% de la población entre m ± 2 s, y el 99% entre m ± 3 s, aproximadamente.
Con unos mínimos cálculos, sabemos que el 68% de nuestros adolescentes tendrán una presión entre 108 y 132 mmHg, el 95% entre 96 y 144 mmHg y el 99% entre 84 y 156 mmHg. Además, solo un 2,5% de la población tendrá una presión menor de 96 mmHg y otro 2,5%, mayor de 144 mmHg.
Por último, podríamos hacer una estimación del valor en la población de la que procede la muestra calculando su intervalo de confianza.
El intervalo de confianza al 95% de una media se calcula según la siguiente fórmula:
IC 95 = m ± 1,96 ee
ee representa el error estándar de la media, que se calcula, a su vez, dividiendo la desviación estándar entre la raíz cuadrada del tamaño muestral.
Así, podemos hacer ya el cálculo:
IC 95 = 120 ± 1,96 x (12/raíz de 1000)
Si resolvemos la ecuación anterior, obtenemos que, con una confianza del 95%, el valor poblacional de presión arterial sistólica en los adolescentes estará entre 119,25 y 120,74 mmHg.
Para los muy puristas, asumimos que conocemos la varianza poblacional y que es igual a la de nuestra muestra. En caso contrario tendríamos que haber utilizado la cuasi-desviación típica o, mejor, utilizado una distribución de la t de Student para calcular el intervalo (aunque con una muestra tan grande nos va a dar lo mismo).
Paso 3. Cálculo de probabilidades
Imaginemos que estamos interesados en saber el porcentaje de la población que incluye un determinado intervalo de presión. Por ejemplo, entre 90 y 135 mmHg. Dicho de otra forma, qué probabilidad existe de que un individuo seleccionado al azar tenga una presión arterial sistólica entre 90 y 135 mmHg.
Vamos a calcularlo con R a través del menú Distribuciones-> Distribuciones continuas->Distribución normal->Probabilidades normales acumuladas…:
– Menor de 90 mmHg: marcamos 90 en la casilla “valor(es) de la variable”, 120 en “media” y 12 en “desviación típica”. ¿Qué cola seleccionamos? Como queremos la probabilidad de los valores menores de 90, seleccionamos la cola izquierda. R nos dice que la probabilidad es de 0,0062.
– Mayor de 135 mmHg: marcamos 135 en la casilla “valor(es) de la variable”, 120 en “media” y 12 en “desviación típica”. ¿Qué cola seleccionamos? Como queremos la probabilidad de los valores mayores de 135, esta vez seleccionamos la cola derecha. R nos dice que la probabilidad es de 0,1056.
Como la probabilidad total es 1 (100%), sabemos que P(<90) + P(90-135) + P(>135) = 1. Si despejamos, obtenemos que P(90-135) = 0,8882. Redondeando, el 89% de nuestros adolescentes tiene una presión arterial sistólica entre 90 y 135 mmHg.
Dicho de otro modo, si extraemos un individuo al azar, existe una probabilidad de 0,89 (89%) de que su presión arterial esté en el rango comprendido entre 90 y 135 mmHg.
Paso 4. Estandarizar simplifica los cálculos.
La distribución normal estándar es aquella que tiene una media de 0 y una varianza de 1, y que se suele representar como N(0,1).
La gran ventaja es que facilita muchos los cálculos. En nuestro ejemplo, a priori no sabemos cuántos jóvenes tendrán una presión arterial mayor de 144 mmHg. Sin embargo, en una distribución estándar sabemos, sin necesidad de calcular, que la probabilidad de tener más de 2 (que es lo mismo que más de 2 desviaciones estándar) es de 0,025 (2,5%).
Visto lo anterior, es fácil comprender que será más sencillo calcular las probabilidades de los valores estandarizados. Para ello, se le resta a cada valor la media de la distribución y se divide por la desviación estándar. Calculamos así lo que habitualmente llamamos puntuación z, que representa el número de desviaciones estándar que cada valor se separa de la media de la distribución.
Así, para 90, el valor z = -2,5; para 135, z = 1,25. Ya sabemos, de un vistazo, que será muy raro que tengan menos de -2,5 y que no habrá mucho más allá de un 10% por encima de 1,25. Así, la proporción de los que están dentro del intervalo de -2,5 a 1,25 estará alrededor del 90%.
Claro que esto no se hace para redondear. Podemos utilizar el mismo método que antes para calcular el valor exacto de la probabilidad. Hacedlo y veréis como sale lo mismo.
La ventaja, además de ser más intuitiva cuando se conocen las características de la distribución normal, es que, en el caso de no tener un ordenador a mano, con una sola tabla de probabilidades podemos hacer los cálculos para cualquier distribución normal que se nos ocurra. Solo tendemos que estandarizarla.
Nos vamos…
Hemos visto cómo comprobar que nuestros datos siguen una distribución normal y, así, poder calcular la probabilidad de encontrar determinados valores.
Pero, ¿qué ocurre si nuestros datos no son normales? Pues tendríamos varias opciones, desde intentar transformarlos hasta utilizar otras distribuciones de probabilidad. Pero esa es otra historia…
Bibliografía
– Solanas A, Selvam RM. Distribuciones de probabilidad. En: Peró Cebollero M, Leiva Ureña R, Guardia Olmos J, Solanas Pérez A, eds. Estadística aplicada a las ciencias sociales mediante R y R-Commander. Garceta Publicaciones SL. Madrid, 2012; p:111-64.
– Introductory statistical principles. En: Logan M, ed. Biostatistical design and análisis using R. A practical guide. John Wiley & Sons Inc. Publication. Oxford, 2010; p:65-75. (PDF)