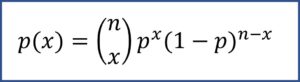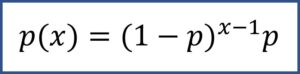Manuel Molina Arias.
Servicio de Gastroenterología.
Hospital Infantil Universitario La Paz.
Madrid. España.
Todos estaremos de acuerdo en lo agradable que resulta llegar al final del día totalmente agotado, meterte en la cama y dormirte en cuestión de segundos. Os puedo decir que yo, la mayor parte de las veces, al día siguiente ni me acuerdo del momento de acostarme.
Claro que esto no ocurre siempre así. Hay veces que el cerebro se empeña en seguir funcionando, a veces por preocupaciones de nuestra vida diaria, pero otras veces se empeña en los pensamientos más inútiles y absurdos, a pesar de que el resto del cuerpo pide a gritos la desconexión.
Para estos días, o noches, aciagos en los que no podáis conciliar el sueño, yo os recomiendo un remedio infalible: contar ovejas.
No falla prácticamente nunca. El secreto es contarlas sin prestarle mucha atención a las ovejas que van pasando por encima de la almohada y no obsesionarse con el tamaño del rebaño que se va acumulando debajo de la cama. Y, mucho menos, por el tipo de ovejas que hemos contado.
Y os digo esto último para que no cometáis el error de mi primo. El pobre es insomne y, siguiendo mi consejo, empieza a contar ovejas. El problema es que, como es de vocación naturalista, empieza a fijarse en el color de cada oveja, en si tiene el pelo largo, si es churra o es merina, y cosas por el estilo.
Y ahí no queda la cosa, empieza a calcular la probabilidad de que las próximas ovejas sean de un tipo o de otro. ¿Queréis saber cómo lo hace? Seguid leyendo y lo veréis.
Distribuciones de probabilidad
Ya sabemos que la probabilidad mide el grado de incertidumbre o de posibilidad de ocurrencia de cada uno de los resultados posibles de un suceso. Esto suele calcularse en los casos más sencillos dividiendo el número de sucesos favorables entre el número de sucesos posibles.
Por ejemplo, si tiramos un dado de seis caras, la probabilidad de que salga un dos será de 1/6. Así, la probabilidad puede tener un valor entre 0 (es imposible que se produzca el suceso) y 1 (es seguro que se produce el suceso).
Pero no siempre el cálculo de la probabilidad de un suceso es tan sencillo. Para los cálculos más complejos, lo habitual es recurrir a la distribución de probabilidad que sigue el suceso en la población.
La distribución de probabilidad es aquella que permite establecer toda la gama posible de valores del suceso, que suele ser una variable aleatoria, por lo que permite establecer la probabilidad de que el suceso ocurra al realizar un experimento determinado.
Distribuciones de probabilidad discretas
Ya sabemos que las variables aleatorias pueden ser continuas o discretas. De igual modo, las distribuciones de probabilidad son también continuas o discretas, en función del tipo de variable de la que expliquen su distribución.
La más conocida de estas distribuciones de probabilidad es, sin duda, la distribución normal, que es una distribución de probabilidad continua.
Sin embargo, mi primo, para sus cábalas con las ovejas, utiliza distribuciones de probabilidad discretas, que son a las que tenemos que recurrir cuando queremos contar objetos. Esto es así porque las variables aleatorias discretas son las que describen las variables con valores enteros, con o una lista de valores positivos y/o negativos.
Hay numerosas distribuciones de probabilidad discreta, pero aquí nos vamos a centrar en las favoritas de mi primo y en ver cómo las usa. Estas son la distribución de Bernoulli, la distribución binomial, la distribución geométrica y la distribución hipergeométrica.
Distribución de Bernoulli
La distribución de Bernoulli, también llamada distribución dicotómica, se utiliza para representar una variable aleatoria discreta que solo puede tener dos resultados mutuamente excluyentes. Además, solo podemos aplicar esta distribución cuando realicemos un solo experimento. Si hacemos varios, tendremos que recurrir a la distribución binomial, que veremos más adelante.
Estos dos resultados de un experimento de Bernoulli se suelen denominar éxito y no éxito. Aquí es importante tener en cuenta que “no éxito” no significa lo contrario de éxito, sino cualquier otro resultado diferente a éxito.
Por ejemplo, si definimos un experimento de Bernoulli tirando un dado y considerando éxito sacar un 6, el no éxito será sacar 1, 2, 3, 4 o 5.
Como todas las distribuciones de probabilidad, podemos definir la distribución de Bernoulli en función de algunos de sus parámetros. Así, si la probabilidad de éxito es “p” y la de no éxito “1-p”, la distribución puede definirse por su media (p) y su varianza (p(1-p)).
Esta distribución es la más sencilla. Supongamos que entre las ovejas que cuenta mi primo hay un 25% de churras, un 30% de merinas, un 15% de ovejas de Carranza y, el resto, manchegas.
Para saber cuál es la probabilidad de que la próxima oveja que cruce su almohada sea de Carranza, solo tiene que aplicar la ley de Laplace de los casos favorables divididos por los casos posibles. En este caso, 15/100 = 0,15.
Distribución binomial
La cosa se le complica un poco a mi primo si quiere calcular probabilidades con más de una oveja, ya que entonces no le valen los experimentos de Bernoulli. Por ejemplo, imaginemos que quiere saber qué probabilidad tiene de contar 3 churras entre las primeras 15 ovejas.
Para un caso así, mi primo recurre a la distribución binomial. Es parecida a la de Bernoulli, pero nos dice la probabilidad de obtener un resultado entre dos posibles al realizar un número n de experimentos.
Para los amantes de las fórmulas, siendo p la probabilidad de éxito, la forma general para calcular la probabilidad binomial es la que podéis ver en la figura 1.
Como podemos ver en la fórmula, para caracterizar una distribución de probabilidad binomial solo necesitamos el número de experimentos (n) y la probabilidad de éxito (p). Su media se puede calcular como np y su varianza como np(1-p).
Volvamos al problema de mi primo. Quiere saber qué probabilidad hay de que pasen un mínimo de 3 churras entre las primeras 15 ovejas. En este caso, n = 15 y p = 0,25 (un 25% de las ovejas). Para saber el valor de la probabilidad, solo necesitamos sustituir los valores en la fórmula anterior y resolverlo, pero vamos a pedirle al programa R que lo haga por nosotros:
1- pbinom(3, 15, 0.25)
R nos dice que la probabilidad es de 0,54. Si queremos saber la probabilidad de que pasen menos de 3, calculamos el complementario del valor actual: 1 – 0,54 = 0,46. También se lo podemos preguntar a R:
pbinom(3, 15, 0.25)
Distribución geométrica
Llegadas las tres de la madrugada, mi primo empieza a hacerse preguntas más delirantes. Por ejemplo, si las ovejas de Carranza son las menos frecuentes (el 15%), ¿cuál es la probabilidad de que no aparezca una oveja de Carranza hasta que ya hayan pasado 9 de otras razas?
Aquí no nos vale ninguna de las dos distribuciones anteriores. Para resolver este problema necesitamos la distribución geométrica, útil para cuando se repiten pruebas en espera de un suceso determinado.
La distribución geométrica es una distribución discreta que nos permite calcular la probabilidad de que haya que realizar un número k de experimentos para que se produzca un suceso, siendo p la probabilidad del suceso.
Si lo pensamos un poco, la probabilidad será cada vez menor a medida que aumente k. Cada vez será menos probable tener que esperar un número de experimentos mayor para observar un éxito. Por esta razón la distribución geométrica está muy sesgada hacia la derecha. Para aquellos a los que pueda interesar, la media se define como 1/p y la varianza como 1-p/p2.
Vamos a resolver el problema de mi primo. La probabilidad de ver una oveja de Carranza es de 0,15, así que la probabilidad de que sea de otra raza es de 1 – 0,15 = 0,85. Además, tengamos en cuenta que cada oveja (cada experimento) es independiente de la anterior o la posterior.
Así, empezamos calculando la probabilidad de ver otras razas en los 9 primeros intentos: multiplicaremos las probabilidades de cada suceso independiente, o sea, 0,85^9 = 0,23. Terminamos ahora de calcular la probabilidad de 9 “no éxitos” (otra raza) y de un éxito (Carranza): 0,23 x 0,15 = 0,03.
Si habéis entendido el cálculo anterior, comprenderéis la fórmula de la probabilidad geométrica (Fig 2), que nos hubiese permitido hacer el cálculo directamente.
Pero mi primo no queda contento con este resultado y se pregunta cuántas ovejas tienen que pasar, por término medio, para ver tres de Carranza. Como ya hemos dicho, la media es 1/p, así que 3x(1/0,15) = 20: tendrán que pasar unas 20 ovejas para que tres sean de Carranza.
De todas formas, lo recomendable es hacer los cálculos de probabilidad geométrica con una calculadora o un programa estadístico. Vamos a preguntarle a R cuál es la probabilidad de que no aparezca ninguna oveja de Carranza hasta la décima oveja que contemos:
dgeom(10, 0.15)
R nos da el mismo valor, 0,03. Hay un 3% de probabilidades de que no aparezca una oveja de Carranza hasta la décima oveja de nuestra noche insomne.
Distribución hipergeométrica
Y vamos a ir acabando nuestra noche en vela con la pregunta que angustia a mi primo a eso de las cinco de la mañana: de las 35000 ovejas que ya hay debajo de la cama, si elegimos 100 al azar, ¿cuál es la probabilidad de que, como máximo, 22 sean churras?
Para esto hay que recurrir a la última de las distribuciones de las que vamos a hablar hoy: la distribución hipergeométrica.
La distribución hipergeométrica es una distribución de probabilidad discreta útil para aquellos casos en los que se extraen muestras o en los que hacemos experimentos repetidos sin reemplazo del elemento que hayamos extraído. Vemos, pues, que se ajusta a este problema.
Si partimos de una población de N elementos, N1 serán éxitos y N2 serán fracasos (no éxitos), teniendo en cuenta que cada elemento solo puede pertenecer a uno de los dos grupos. Si obtenemos una muestra n sin reemplazo (no son extracciones independientes), podemos calcular la probabilidad de obtener un determinado número de éxitos.
En nuestro ejemplo, N = 35000. El número de éxitos (ser churra) será de 35000×0,25 (el 25% de las ovejas son churras), esto es, 8750 ovejas churras. Utilizaríamos R para calcular la probabilidad de que haya un máximo de 22 churras en nuestra muestra de 100 ovejas:
phyper(22, 8750, 35000-8750, 100)
El resultado es 0,28: hay un 28% de probabilidad de que, si extraemos al azar 100 ovejas, haya, al menos, 22 churras.
En resumen
Como podemos ver, las cuatro distribuciones de probabilidad que hemos empleado son distribuciones discretas útiles para cuando hacemos recuentos al ser la variable aleatoria de tipo discreto.
¿Cuándo usamos cada una de ellas? Cuando sean experimentos únicos con un resultado dicotómico la elección es sencilla: distribución de Bernoulli. Cuando se trate de experimentos independientes múltiples y queramos saber la probabilidad de un determinado número de éxitos, utilizaremos la probabilidad binomial.
Otras veces querremos saber el número de experimentos que tendremos que realizar para tener un éxito: nuestra herramienta en estos casos será la distribución geométrica. Por último, cuando hagamos extracciones sin reemplazo de una muestra y queramos saber la probabilidad de obtener un tipo u otro de elemento, necesitaremos recurrir a la distribución de probabilidad hipergeométrica que, para quien no lo sepa, es la que está detrás de la prueba exacta de Fisher.
Nos vamos…
Y aquí lo vamos a dejar por hoy. No creáis que mi primo cae rendido al sueño después del último problema que resolvimos.
Nada más lejos de la realidad.
En su insomnio pertinaz, cuando el sol comienza a despuntar por el horizonte, mi primo riza el rizo con sus problemas con las ovejas y se pregunta cuántas ovejas tendrá que contar para que entre en su rebaño la décima oveja manchega. Para esto necesita utilizar una distribución de la que no hemos hablado hoy y a la que volveremos en otra ocasión: la distribución binomial negativa. Pero esa es otra historia…
Bibliografía
– Toledo E, Sánchez-Villegas A, Martínez-González MA. Probabilidad. Distribuciones de probabilidad. En: Martínez-Sánchez MA, Sánchez-Villegas A, Toledo EA, Faulin J, eds. Bioestadística amigable, 3ª ed. Elsevier España, SL. Madrid, 2014; 65-100. (HTML)
– Mathematics. En: Crawley MJ ed. The R book. John Wiley and Sons Ltd. West Sussex, Inglaterra, 2017; 259-343. (PDF)