Un baile épico. Técnicas de regularización en regresión múltiple.

Creo que, últimamente, paso más tiempo del que debiera deambulando por un lejano y misterioso rincón del mundo de la estadística, donde se lleva a cabo un baile épico que ha dejado a muchos entendidos perplejos y, en ocasiones, tambaleándose. Ese rincón al que me refiero es el de la regresión múltiple, allí donde los números bailan al ritmo de los datos y las ecuaciones se enredan en un torbellino matemágico.

A nadie le extrañará, pues, que al dormirme me asalten pesadillas irreales y angustiosas, dignas de un oscuro relato de Lovecraft. Sin ir más lejos, la otra noche soñé que asistía a una fiesta elegante de datos. Los números iban vestidos con sus mejores atuendos gaussianos, las ecuaciones charlaban en grupos y las variables independientes trataban de impresionar a las dependientes.

En el centro de la pista de baile, el pinchadiscos hacía girar los vinilos de las distribuciones de probabilidad mientras que los modelos de regresión hacían su entrada triunfal. Es, en ese momento, cuando mi mirada se fijó en uno de los rincones de la sala, atraída por una pareja deslumbrante. Ella era la estrella de la noche, la diva del descenso del gradiente, la reina de la regularización. Con su atuendo de penalización y su actitud de restricción, la Regularización LASSO estaba acompañada por Ridge, el galán de mirada intensa que se deslizaba hacia modelos menos sobreajustados. Ambos se disponían a entrar en la pista de baile.

Me desperté sobresaltado y empapado en sudor, con la respiración entrecortada. Me fue imposible volver a conciliar el sueño esa noche, así que me puse a investigar cómo podrían mis modelos encontrar el equilibrio entre la extravagancia del ajuste excesivo y la rigidez de la subestimación. Si alguno de vosotros está interesado en conocer los resultados de este desvarío, le invito a seguir leyendo esta entrada.

Las tribulaciones de la regresión múltiple

La regresión lineal es un método estadístico para modelar la relación entre una variable dependiente y una o más variables independientes. El objetivo es encontrar la ecuación que mejor se ajuste a los datos para predecir los valores de la variable dependiente en función de los valores de las variables independientes.

Habitualmente, esto se consigue mediante el método de los mínimos cuadrados (también llamado mínimos cuadrados ordinarios), que trata de minimizar las diferencias entre los valores observados de la variable dependiente y los valores predichos por el modelo, diferencias que se conocen con el apelativo de residuos. Los residuos se elevan al cuadrado (para que no se cancelen los positivos con los negativos) y se suman. La mejor ecuación de regresión será aquella en la que esta suma de los cuadrados de los residuos tenga el valor más bajo.

Aunque este método consiga un modelo que tenga un buen ajuste a los datos con los que se ha elaborado, puede que este no sea tan bueno cuando trate de predecir los valores de la variable independiente con datos nuevos, diferentes a los utilizados durante su elaboración. Esto puede ocurrir cuando se dan una serie de circunstancias.

La primera es la colinealidad, que se produce cuando hay alta correlación entre las variables predictoras o independientes. Esto puede ocasionar que algunos de los coeficientes de regresión tomen valores excesivamente elevados o bajos, de signo contrario al que pudiéramos esperar por nuestros conocimientos del modelo, o con errores estándar llamativamente elevados.

En esta situación, incluso si tenemos suerte de que el modelo pueda hacer predicciones más o menos correctas, será difícil su interpretación y la de la importancia de cada variable para explicar la variabilidad global.

Otro problema que puede presentarse es el de la alta dimensionalidad o, dicho de forma más sencilla, la existencia de un número elevado de variables independientes en el modelo. En general, los modelos más complejos tienen tendencia al sobreajuste de los datos (overfitting): se ajustan bien con los datos conocidos, pero fracasan a la hora de generalizarse a datos nuevos.

Esto alcanza el límite en el caso de que el número de variables independientes se acerque al número de participantes (tamaño muestral), en el que el método de los mínimos cuadrados puede fracasar en la obtención de los coeficientes de regresión.

Pues bien, para aliviar o solucionar estos problemas, disponemos de una serie de técnicas de regularización. ¿Os acordáis de mi sueño y de la pareja que me hizo despertar? Pues sí, estas dos técnicas son la regularización de cresta (más conocida como ridge) y la regularización de lazo (lasso, en realidad).

Bueno, hay también una tercera que comparte herencia de estas dos: la regularización en red elástica. Vamos a ver en qué consisten.

Técnicas de regularización

Las técnicas de regularización nos ayudan a minimizar los problemas que hemos descrito realizando restricciones en los coeficientes de regresión del modelo, lo que ayuda a controlar su complejidad y a evitar que los coeficientes tomen valores extremos.

Como ya hemos dicho, las dos técnicas de regularización más comunes son la regresión ridge (permitidme que use el término en inglés, que está consagrado por su uso), también llamada regularización L2, y la regresión lasso (Least Absolute Shrinkage and Selection Operator) o regularización L1.

Ambas técnicas se basan en realizar una modificación del método de los mínimos cuadrados ordinarios añadiendo una penalización a la suma de los cuadrados de los residuos. Esto tiene como resultado una restricción de los coeficientes del modelo, lo que ayuda a controlar su complejidad, aumenta la estabilidad de los coeficientes y evita sus valores extremos.

Regresión ridge

La regresión ridge trata de minimizar el error de predicción agregando, a la función de coste original (suma de los cuadrados de los residuos), un término de penalización proporcional al cuadrado de los coeficientes. La fórmula sería la siguiente:

Función de coste modificada = coste original + λ x Σ(coeficientes²)

El valor del parámetro λ es determinado por el investigador y debe ser mayor que cero, ya que si λ = 0 no existe diferencia con la regresión lineal múltiple sin regularización.

Cuanto mayor sea el valor de λ, mayor será la restricción que se impone al modelo.

Si lo pensamos un poco, el elevar los coeficientes al cuadrado hace que se penalice más a los coeficientes con un valor absoluto mayor. El resultado cuando, por ejemplo, existe colinealidad, es aproximar los valores extremos a valores intermedios. Los coeficientes se aproximan a cero, pero sin llegar a este valor (como veremos que ocurre en la regresión lasso), por lo que no llegan a desaparecer de la ecuación, aunque sí disminuye su impacto en el modelo global.

Regresión lasso

La regresión lasso también agrega un término de penalización a la función de coste original, pero, en este caso, es proporcional al valor absoluto de los coeficientes y no a su valor al cuadrado:

Función de coste modificada = coste original + λ x Σ|coeficientes|

La regresión lasso restringe la magnitud de los coeficientes de regresión, pero, a diferencia de la regresión ridge, sí que pueden llegar al valor cero, lo que implica que llegan a desaparecer del modelo. Esto es muy útil para disminuir la complejidad del modelo y cuando se necesita realizar una reducción de la dimensionalidad, que no es otra cosa que disminuir el número de variables independientes.

Nuevamente, cuando λ = 0, el resultado es equivalente al de un modelo lineal por mínimos cuadrados ordinarios. A medida que aumenta el valor de λ, mayor es la penalización y más variables predictoras pueden quedan excluidas del modelo.

Diferencias entre regresión ridge y regresión lasso

Aunque ambas técnicas disminuyen la magnitud de los coeficientes de regresión, solo la regresión lasso consigue que algunos sean exactamente cero, lo que posibilita realizar selección de variables predictoras. Esta es la mayor ventaja de la regresión lasso cuando trabajamos con escenarios en los que no todas las variables predictoras son importantes para el modelo y queremos que las menos influyentes queden excluidas.

Por su parte, la regresión ridge resulta de mayor utilidad cuando existe colinealidad entre variables independientes, ya que reduce la influencia de todas ellos al mismo tiempo y de forma proporcional. También podemos utilizarla si nos encontramos ante un supuesto en el que perder variables independientes sea un lujo que no nos podamos permitir. 

No obstante, podemos encontrarnos con situaciones en las que no tengamos claro cuál de las dos técnicas utilizar o en las que queramos aprovechar las ventajas de las dos. Para conseguir un equilibrio entre las propiedades de las dos, podemos recurrir a la que se conoce como regresión de red elástica.

Regresión de red elástica: el punto medio

Esta técnica combina la penalización de las técnicas de regularización L1 y L2, lo que intenta aprovechar las ventajas de ambas y soslayar algunos de sus inconvenientes. La fórmula sería la siguiente:

Función de coste nueva = coste original + [(1 – α) x λ x Σ(coeficientes²)] + (α x λ x Σ|coeficientes|)

Para entenderla un poco mejor, podemos escribirlo más simplificado:

Función de coste nueva = coste original + (1 – α) penalización L2 + α x penalización L1

Como podéis ver, ahora tenemos dos coeficientes, α y λ. Los valores de α oscilan entre 0 y 1. Cuando α = 0, la técnica sería equivalente a hacer una regresión ridge, mientras que, cuando α = 1, funcionaría como una regresión lasso. Valores intermedios nos marcarían una posición de equilibrio entre las dos técnicas de regularización.

Así que, cómo es fácil de comprender, tenemos que decidir los valores de α y λ para saber qué grado de penalización aplicar y qué predominio de las dos técnicas utilizar. Esto suele hacerse probando muchos valores y viendo cuál es el que mejores resultados nos da, proceso del que suelen hacerse cargo los programas de estadística que empleamos para estas técnicas.

Un ejemplo práctico

Creo que es el momento de poner un ejemplo práctico de todo lo que hemos hablado hasta ahora. Nos va a permitir entenderlo mejor y comprender cómo se realiza en la práctica. Para ello, vamos a utilizar un programa estadístico concreto, el programa R, y uno de sus conjuntos de datos más utilizados con fines docentes, el mtcars.

Este conjunto de datos contiene información sobre diferentes modelos de automóviles y sus características. Incluye 32 filas (una por cada modelo de automóvil) y 11 columnas que representan diversas características de los automóviles, como la eficiencia del combustible (mpg), el número de cilindros (cyl), la cilindrada (disp), la potencia del motor (hp), la relación de ejes traseros (drat), el peso (wt), el tiempo en cuarto de milla (qsec), etc.

No voy a detallar todos los comandos que hay que ejecutar para este ejemplo, ya que este baile podría alargarse hasta altas horas de la madrugada, pero si hay alguien interesado en reproducir el ejercicio puede ver o descargarse el script completo en este enlace.

Vamos a ver el proceso paso a paso.

1. Carga de bibliotecas de funciones y preparación de datos

En R, lo primero que hacemos es cargar las bibliotecas o librerías que vamos a necesitar para el procesado de los datos, su representación gráfica y la elaboración de los modelos de regresión lineal múltiple y de las técnicas de regularización.

A continuación, cargamos el conjunto de datos. Preparamos un vector con la variable dependiente y una matriz con las independientes, ya que vamos a necesitarlas para aplicar las funciones que realizan la regularización.

2. Modelo de regresión lineal

Empezamos elaborando el modelo de regresión lineal tomando la potencia del motor (hp) como variable dependiente y el resto de las variables como independientes o predictoras.

Centrándonos en los resultados que nos interesan para nuestro ejemplo, el modelo es estadísticamente significativo (F = 19.5 con 10 y 21 g.l., p < 0.05) y explica un 85% de la varianza de la variable dependiente (R² ajustado = 0.85). Pero lo más interesante es fijarnos en la figura 1 con los coeficientes de regresión.

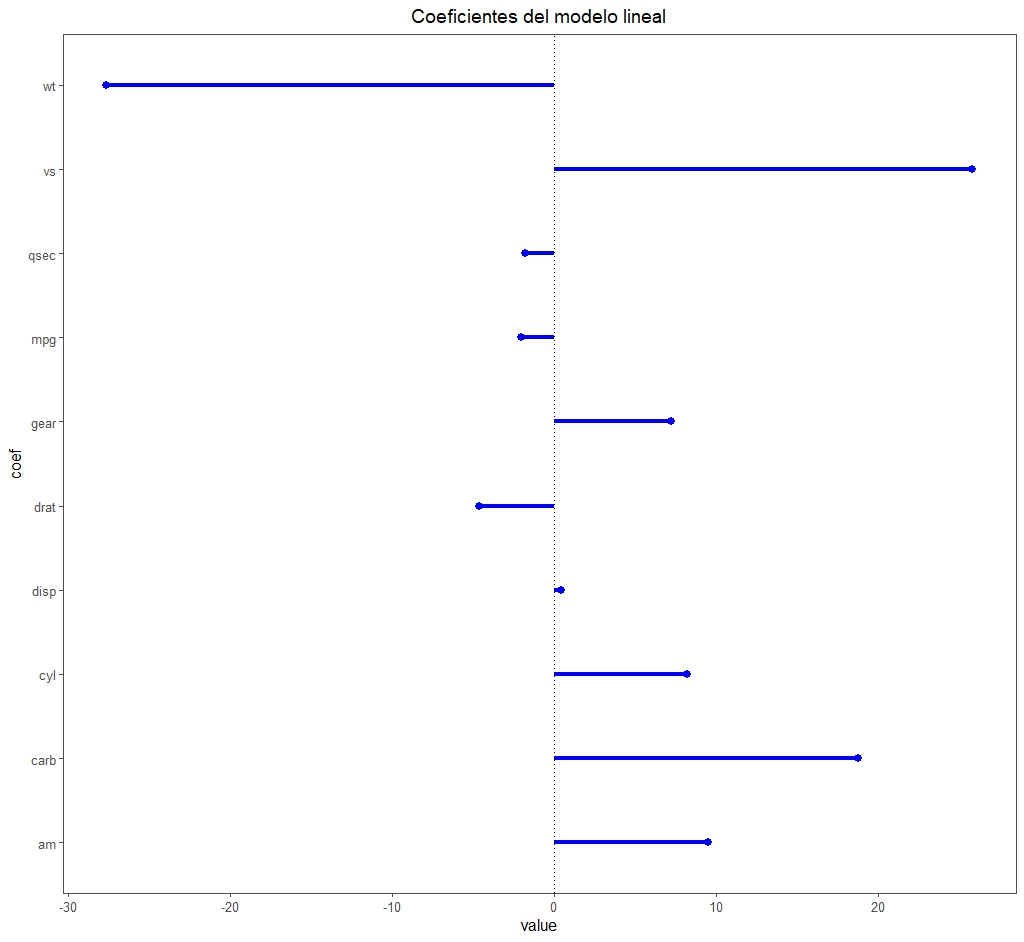
Veis que hay algunos que llaman la atención por su magnitud respecto a los demás, como los de las variables wt y ws.

Este puede ser un signo de que existe colinealidad. Además, el modelo tiene un número elevado de variables predictoras para el tamaño muestral (solo 32 registros), por lo que el riesgo de sobreajuste es elevado. Decidimos aplicar técnicas de regularización.

3. Regresión ridge

Si usamos R, podemos realizar técnicas de regularización con la función glmnet(), ajustando el valor de su parámetro alpha. Para que realice una regresión ridge, establecemos el valor de alpha = 0.

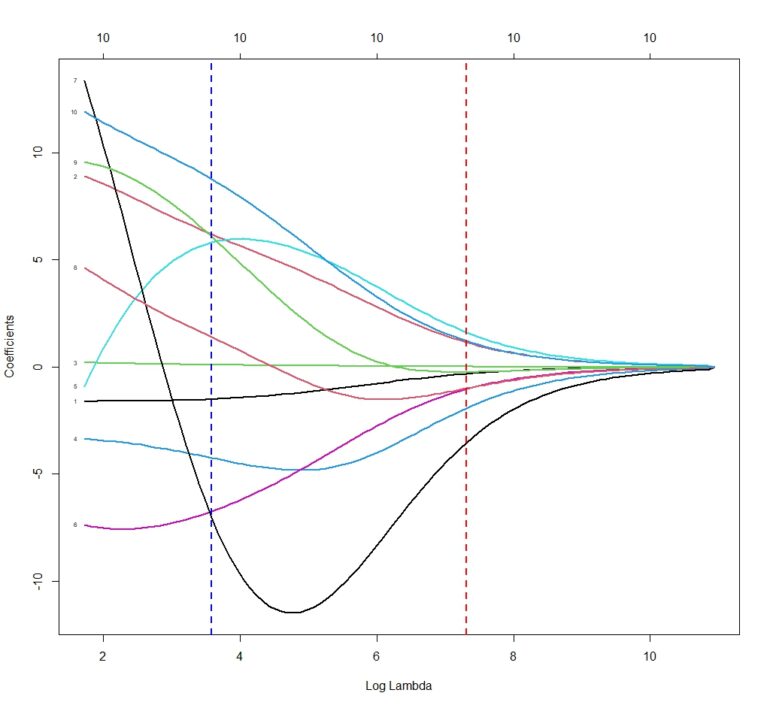
Ya hemos dicho que tenemos que elegir el valor de λ que nos interesa aplicar. ¿Y cómo lo sabemos? R nos ayuda en esta tarea. La función glmnet() no calcula un solo modelo, sino muchos (100, si no le indicamos otra cosa) con distintos valores de λ. Cada uno de estos modelos tendrá sus coeficientes de regresión diferentes, cómo podéis ver en la figura 2.

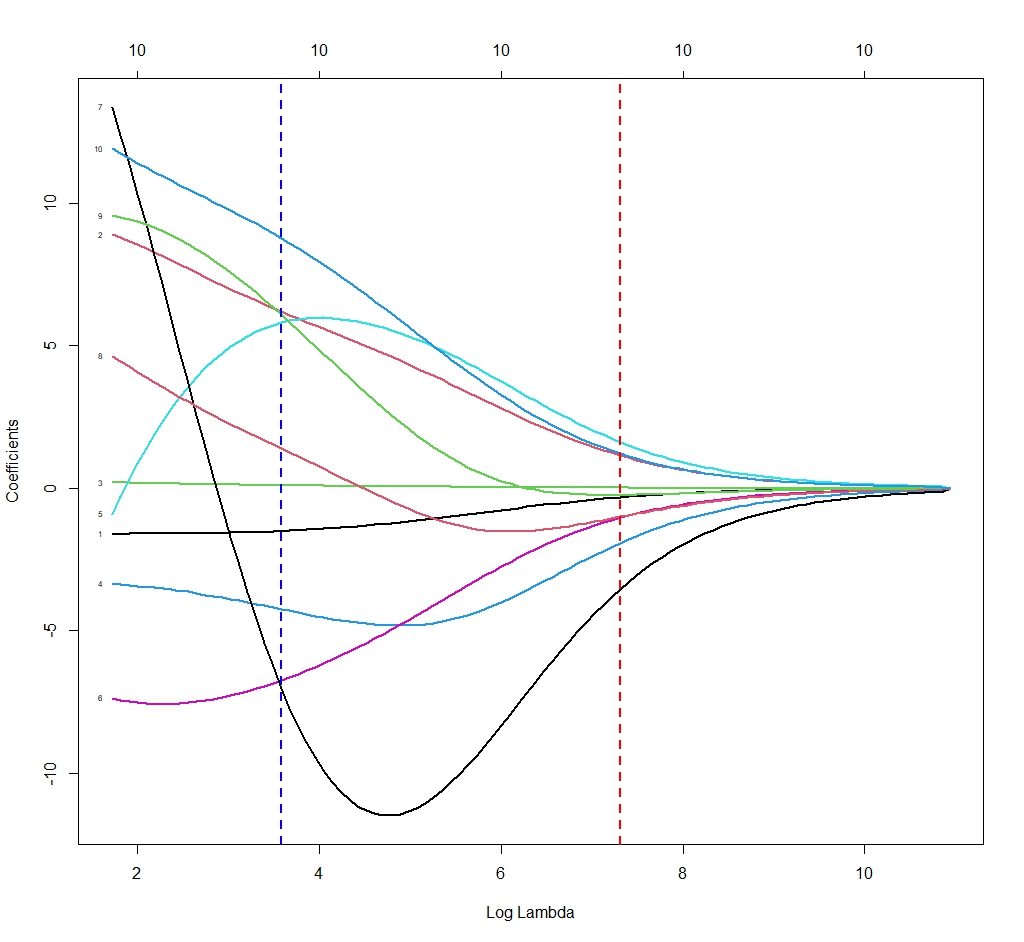
Cada línea del gráfico muestra cómo varía el coeficiente de regresión de cada variable en función del valor de λ. Por ejemplo, la línea azul muestra los valores para λ = 3,6 y la línea roja para λ = 7,3.

La función nos contabiliza, además, la función de coste de cada uno de los modelos y nos da dos valores de interés. Uno, el llamado λ mínimo (λmin), que corresponde al valor mínimo de error de predicción del modelo. Dos, el λ correspondiente a un error de predicción de una desviación estándar de la media de todos los modelos (λ1se).

Vamos a tomar el valor de λmin (hay quien piensa que con λ1se hay menos riesgo de sobreajuste). En la figura 3 podéis ver la distribución del error del modelo en función del valor del logaritmo natural de λ.

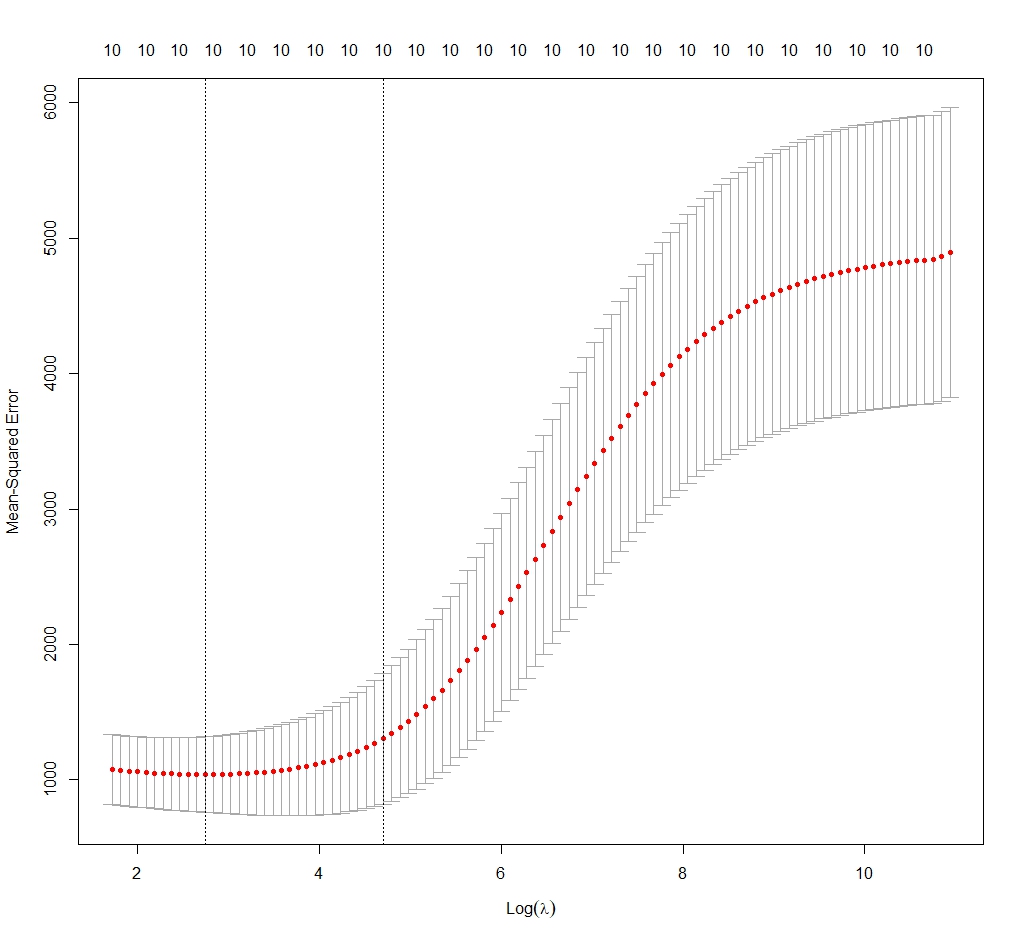
Nos marca los límites óptimos entre las dos líneas verticales. Nos quedamos con nuestro valor de λmin = 2,84.

Fijaos en la figura 4 en la distribución de los coeficientes del modelo correspondiente a λ = 2,84 (que aparecen junto a los del modelo de regresión lasso que elaboraremos más adelante).

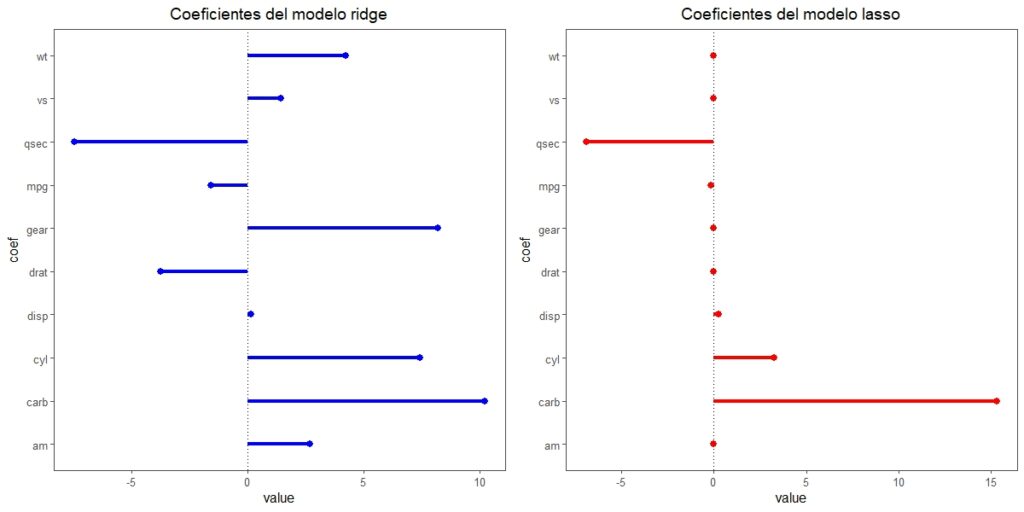
Podemos comprobar cómo la dispersión es menor y cómo ha disminuido también la magnitud de los coeficientes (si la comparáis con las del modelo de regresión lineal, tened en cuenta que las escalas son diferentes, ya que visualmente pueden parecer muy similares).

Ya solo nos queda extraer los valores de los coeficientes de regresión (no tiene interés para lo que estamos tratando). El modelo explica un 87% de la varianza de la variable dependiente (R² = 0.87). Si calculamos su error por el método de los mínimos cuadrados, este es de 24.5.

4. Regresión lasso

Repetiríamos todo el proceso del punto anterior, pero estableciendo alpha = 1 en la función glmnet().

Obtenemos un valor de λmin = 3.5. La distribución de los coeficientes de regresión se muestran en la figura 4. Llama la atención cómo 6 de ellos se han convertido en 0, con lo que desaparecerían del modelo. Esta es, como ya sabemos, una de las características de esta técnica.

Si calculamos el rendimiento del modelo, vemos que es similar al de la regresión ridge, con un valor de R² = 0.87 y un error por mínimos cuadrados de 24.02. Tendremos que decidir cuál de los dos nos interesa más, teniendo en cuenta que, en este caso, la ventaja que podríamos aprovechar es la reducción de la dimensionalidad que proporciona la regresión lasso.

5. Regresión de red elástica.

En este caso tenemos que probar modelos con múltiples valores de α y λ. Esto se realiza en R mediante la función cva.glmnet(), que emplea técnicas de validación cruzada.

Esta función prueba varios valores de α (11, si no le decimos otra cosa) y, para cada uno de ellos, múltiples de λ. Podemos así, de forma similar a los puntos previos, elegir el mejor valor de α y, para este, el valor de λ (en este caso λ1se) que minimiza el error del modelo, como podéis ver en la figura 5.

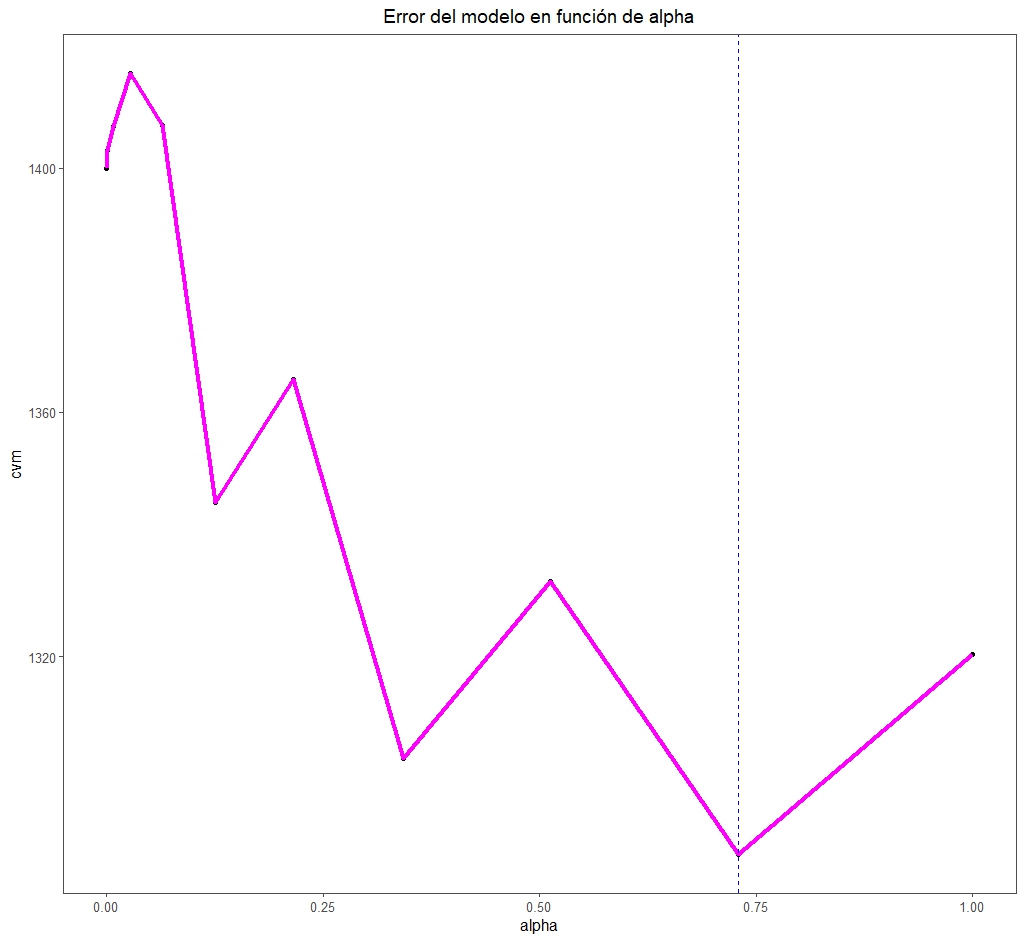
Vemos que el valor de α óptimo es de 0,73. Esto nos marca el punto entre las dos técnicas de regularización, L1 y L2, en los que realizaremos el mejor ajuste.

Nos vamos…

Y con esto vamos a ir terminando por hoy.

Hemos visto cómo las técnicas de regularización de la regresión múltiple pueden ser de gran utilidad cuando tenemos problemas de colinealidad o sobreajuste. Además, pueden servir para seleccionar las variables independientes y reducir la multidimensionalidad, consiguiendo modelos más robustos y fáciles de interpretar.

Antes de despedirnos, quiero aclarar que todo lo que hemos dicho es también válido para la regresión logística múltiple. El modo de realizarlo es similar, aunque puede haber alguna pequeña diferencia en el uso del programa estadístico que empleemos.

En el caso de la regresión logística, la regularización es, además, útil cuando se produce lo que se llama separación o quasiseparación, que ocurre cuando las variables realizan sobreajuste sobre un subconjunto de los datos disponibles para elaborar el modelo. Pero esa es otra historia…

Bibliografía

• Linear and logistic regression. En: Zumel N, Mount J, eds. Practical Data Science with R, 2ª ed. Manning Publications Co. Shelter Island, NY, 2020;215-73. (HTML)
• Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning, 2nd ed. Springer, 2009. (HTML)
• Tibshirani, R. Regression shrinkage and selection via the lasso. J R Stat Soc B Methodol. 1996; 58: 267-88. (PDF)