En el mundo de los números, existe un reino mágico llamado Probabilandia, donde cada rincón está impregnado de la emoción de la estadística y la magia de las probabilidades. Los ríos fluyen con datos, los bosques están llenos de árboles de regresión y, en las montañas, los picos alcanzan alturas proporcionales a su significación estadística.
Uno de los lugares más populares del reino es el majestuoso Palacio de las probabilidades, un casino en el que cada mesa es una aventura estadística y cada carta revela un secreto oculto en los datos. Los jugadores pueden explorar las mesas de juego, desde la ruleta de regresión hasta el póker de pruebas de hipótesis, pasando por la de blackjack de correlación no lineal o la de distribuciones discretas, para los más atrevidos.
Nosotros vamos a detenernos en la mesa de «muestras reducidas», donde las cartas están amontonadas en pequeñas pilas de datos y la incertidumbre alcanza sus cotas más altas. En esta mesa veremos a dos jugadores habituales, la R de Pearson y la z de Fisher.
La R de Pearson, conocida por su elegancia matemática, es como una carta confiable que siempre suma 1. Pero, aunque es ideal para conexiones seguras y lineales, enfrenta desafíos en muestras diminutas, donde la imprecisión puede impactar significativamente su capacidad de estimación, exigiendo precaución extra en la interpretación de los resultados.
En contraste, la z de Fisher, con su toque de intriga estadística, actúa como el comodín que puede cambiar el juego en un instante. Es capaz, aunque la muestra sea reducida, de mantener su precisión con cierta elegancia.
Hoy vamos a quedarnos en este rincón del casino estadístico, donde la R y la z se unen para enfrentar el desafío de muestras reducidas, colaborando en los metanálisis en los que la medida de efecto sea una correlación y los tamaños muestrales de los estudios primarios sean limitados.
El coeficiente de correlación de Pearson
Ya sabemos que uno de los objetivos de un metanálisis es la obtención de una medida global de resultado que resuma los resultados de cada uno de los estudios incluidos en la revisión sistemática. Esta medida proporciona una estimación general del efecto de interés, combinando la información de todos los estudios considerados.
Cuando el efecto estudiado es una correlación, el parámetro que se utiliza con más frecuencia es el coeficiente de correlación producto-momento, más conocido como coeficiente de correlación de Pearson (R).
Podemos calcular R entre dos variables cuantitativas dividiendo la covarianza de las dos variables entre el producto de sus desviaciones estándar, según la primera fórmula de la figura 1 (donde podéis ver todas las fórmulas que vamos a tratar en esta entrada).

Si nos fijamos un poco en la fórmula, R no es más que la covarianza estandarizada por las desviaciones típicas, lo que posibilita comparar diferentes coeficientes de correlación sin que sus valores se afecten por las escalas de medición de las variables.
Este es un punto a favor de la R de Pearson, pero veremos que tiene otras propiedades que no son tan favorecedoras, sobre todo cuando manejamos tamaños muestrales pequeños.
Sabemos que la medida global que calculamos en un metanálisis trata de ser una estimación de esa medida de correlación existente en la población general, que es inabarcable. Para hacer esta estimación, calculamos un intervalo de confianza, habitualmente al 95%, que nos da una idea de la incertidumbre y de los márgenes entre los que puede estar la medida poblacional.
Pues bien, el problema de la R de Pearson es que su varianza depende mucho del tamaño muestral de los datos con los que se ha calculado. Podemos ver su fórmula en la segunda posición del listado de fórmulas.
Lo primero que vemos es que R está en el numerador restando a 1, con lo que el numerador será menor según aumente el valor de R (de forma que la varianza disminuirá). Lo vemos en los diagramas de dispersión si representamos dos variables cuantitativas. Cuando la correlación es mayor, la variabilidad de los datos es menor y la nube de puntos tiene forma más alargada. Cuando la correlación es menor, la nube será más circular, habrá más variabilidad en los datos.
El valor de R no depende de nosotros, sino que es una característica de la relación entre las dos variables cuantitativas. Pero hay otro componente en la fórmula sobre el que sí podemos actuar: el tamaño muestral (n).
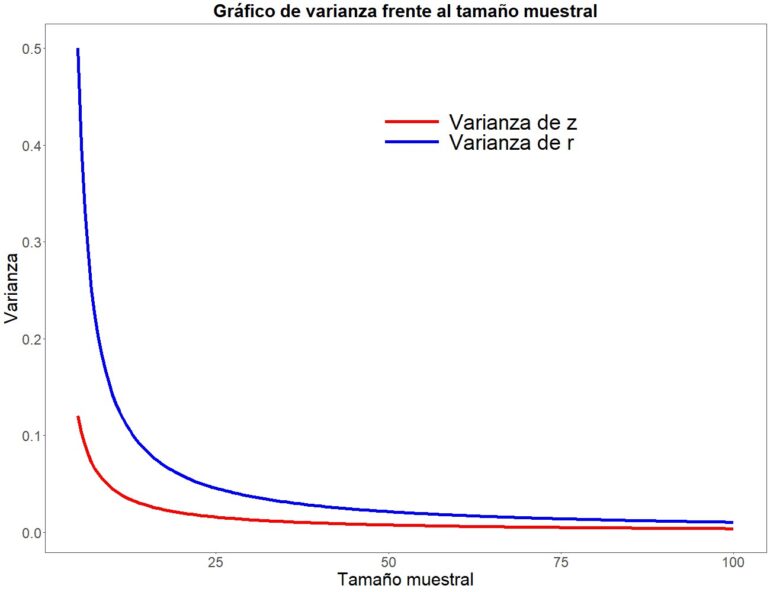
Al estar el tamaño muestral en el denominador, la varianza aumentará al disminuir el tamaño de la muestra. Fijaos en la figura 2, que representa el tamaño muestral en abscisas y la varianza en ordenadas. Centrémonos, de momento, en la línea azul, que representa la varianza de la R de Pearson (luego veremos qué significa la línea roja).
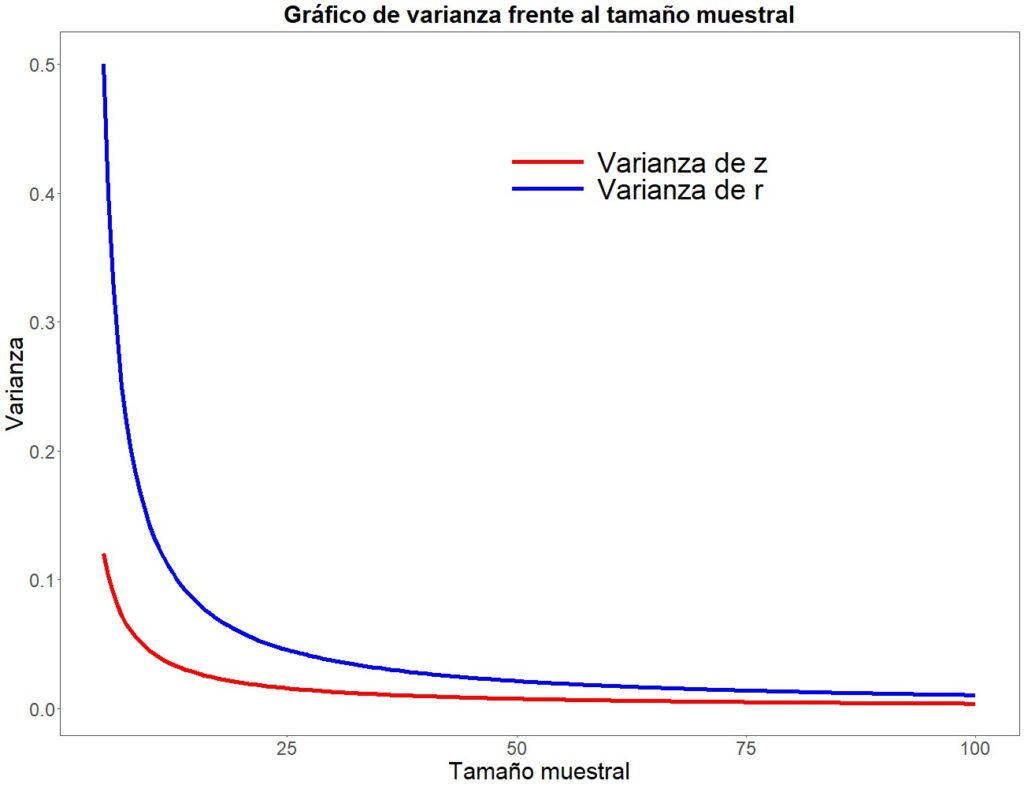
Podemos comprobar cómo la varianza empieza a elevarse al disminuir n, tomando una pendiente muy elevada con tamaños inferiores a 20 participantes. En otras palabras, la varianza se vuelve mayor (más inestable) de forma casi exponencial con los tamaños muestrales más pequeños.
Esto tiene una consecuencia no deseada. Las estimaciones de R se basan en la estimación puntual (el valor de R de cada estudio) y el error estándar (que es la raíz cuadrada de la varianza), por lo que serán más imprecisas cuando el tamaño muestral sea bajo, situación que se nos presenta con relativa frecuencia cuando tratamos con los estudios primarios de un metanálisis.
A medida que el tamaño de la muestra aumenta, las estimaciones del coeficiente de correlación se vuelven más estables y se acercan más a la verdadera correlación poblacional. Sin embargo, en muestras pequeñas, los valores pueden fluctuar más debido al aumento de la variabilidad de las estimaciones.
Dicho de forma más sencilla, y para enfatizar su importancia, el tamaño muestral puede tener un impacto en la interpretación y la fiabilidad de las estimaciones del coeficiente de correlación de Pearson.
Esta es la razón por la cual, en estas situaciones, se aconseja realizar una transformación para obtener la z de Fisher (que no es lo mismo que la z de la distribución normal y la puntuación o score z), que se desenvuelve mejor con muestras pequeñas que la R de Pearson.
Veamos en qué consiste.
La z de Fisher
Como ya hemos dicho, para calcular la medida global cuando los tamaños muestrales son pequeños, en lugar de utilizar directamente la correlación como medida de efecto, se transforma utilizando la función arco tangente hiperbólica inversa, también conocida como la transformación de Fisher.
No os alarméis, detrás de estas palabras tan ofensivas reside una fórmula bastante sencilla, como podéis ver en el listado de la figura 1.
Entenderemos la utilidad de la z de Fisher si nos fijamos, además, en la fórmula para calcular su varianza.
Diréis que sigue teniendo el valor de n en el denominador, como la varianza de R, y que la varianza es mayor cuando el tamaño de la muestra disminuye. Esto es cierto, pero también es lógico que ocurra. Ya sabemos que, en general, y para un mismo nivel de confianza, la precisión de una estimación aumenta (su intervalo de confianza será más estrecho) cuando aumenta el tamaño muestral y/o disminuye la variabilidad, y viceversa.
Pero fijaos ahora en la línea roja de la gráfica anterior que antes decidimos ignorar. Representa la varianza de la z de Fisher en función del tamaño muestral. Aunque vemos que el efecto es similar al que sufre la R de Pearson, su magnitud es mucho menor, con lo que la z se mostrará mucho más precisa que la R cuando la muestra sea pequeña.
La razón detrás de esta transformación está relacionada con las propiedades estadísticas de las distribuciones de probabilidad. Es similar a cuando aplicamos a una serie de datos no normales una transformación como la logarítmica o la inversa para forzar que los datos transformados se distribuyan de forma normal y poder aplicar alguna prueba que asuma la normalidad de los datos.
Al comportarse las correlaciones transformadas de forma más cercana a una distribución normal, los métodos estadísticos basados en la normalidad funcionarán de forma más apropiada. En particular, al realizar un metanálisis, la transformación de Fisher permite combinar los tamaños de efecto de estudios individuales de manera más precisa y adecuada, ya que muchos métodos de metanálisis asumen una distribución normal de los tamaños de efecto.
De todas formas, cuando veamos una publicación sobre uno de estos metanálisis, es probable que no veamos la z por ningún sitio y que los autores solo muestren el coeficiente de correlación de Pearson.
Esto tiene su razón. Lo habitual es utilizar un programa estadístico para realizar el metanálisis. Una de las opciones que podemos indicarle al programa es que realice esta transformación. En ese caso, se transformarán los coeficientes de Pearson de los estudios primarios en sus equivalentes z de Fisher, el programa realizará todos los cálculos con la z de Fisher y, al finalizar, realizará la transformación inversa para presentar al lector el coeficiente de Pearson, que suele ser más fácil de interpretar para la mayoría de los lectores.
Podemos transformar la z de Fisher en su valor de R aplicando la última fórmula del listado que mostramos más arriba.
Un ejemplo práctico
La verdad es que, en la práctica, no nos hace falta prestar mucha atención a todo lo que hemos explicado, ya que los programas de estadística se encargan de estos detalles. De todas formas, no está de más conocer cómo y por qué se hacen las cosas.
Vamos a realizar un ejemplo sencillo de metanálisis con estudios primarios cuya variable de resultado es una correlación. Para ello, vamos a utilizar el programa R (no confundir con el coeficiente de correlación R) y un metanálisis ficticio que nos vamos a inventar sobre la marcha para tratar de estimar la correlación que existe entre los niveles de fildulastrina magnética y los de cafresterol en esa terrible enfermedad que es la fildulastrosis.
Si os animáis, podemos seguir juntos paso a paso.
1. Cargamos las librerías necesarias en R
library(tidyverse)
library(meta)
Si no tenéis instalados estos paquetes, es necesario instalarlos antes de utilizarlos la primera vez mediante el comando install.packages().
2. Crear nuestro conjunto de datos
Vamos a crear un conjunto de datos con 15 estudios totalmente inventados. Para hacer un metanálisis de correlación con R solo necesitamos el valor del coeficiente R de Pearson (no transformado) y el tamaño muestral de cada estudio. Lo añadimos al conjunto de datos, junto con una tercera columna con el nombre del estudio (las letras mayúsculas de la A a la O, para no complicarnos mucho). Creamos las tres variables (vectores en R) y los ensamblamos en un set de datos:
R <- c(0.58, 0.62, 0.54, 0.52, 0.76, 0.69, 0.66, 0.58, 0.62, 0.81,
0.49, 0.60, 0.79, 0.43, 0.69)
N <- c(18, 22, 45, 15, 20, 22, 24, 30, 50, 35, 14, 20, 16, 38, 40)
S <- LETTERS[1:15]
data <- tibble(S, N, R)
3. Hacemos el metanálisis
Vamos a utilizar la función metacor() del paquete meta de R. Aunque esta función admite muchísimos parámetros, vamos a hacer el modelo lo más sencillo posible:
meta <- metacor(cor = R,
n = N,
sm = «zcor»,
studlab = S,
data = data,
comb.fixed = FALSE,
comb.random = TRUE)
Le hemos indicado al programa dónde están los valores de los coeficientes de correlación de Pearson sin transformar (cor), los tamaños muestrales (n) y los nombres de los estudios primarios (studlab), todos dentro del conjunto de datos indicado (data). Por último, le pedimos que aplique un modelo de efectos aleatorios, que haga la transformación de Fisher (sm=”zcor”) y que guarde el resultado en un objeto llamado meta.
4. Obtenemos los resultados
Para ello, simplemente ejecutamos el comando summary(meta).
En la figura 3 podéis ver la salida de resultados que nos ofrece el programa.
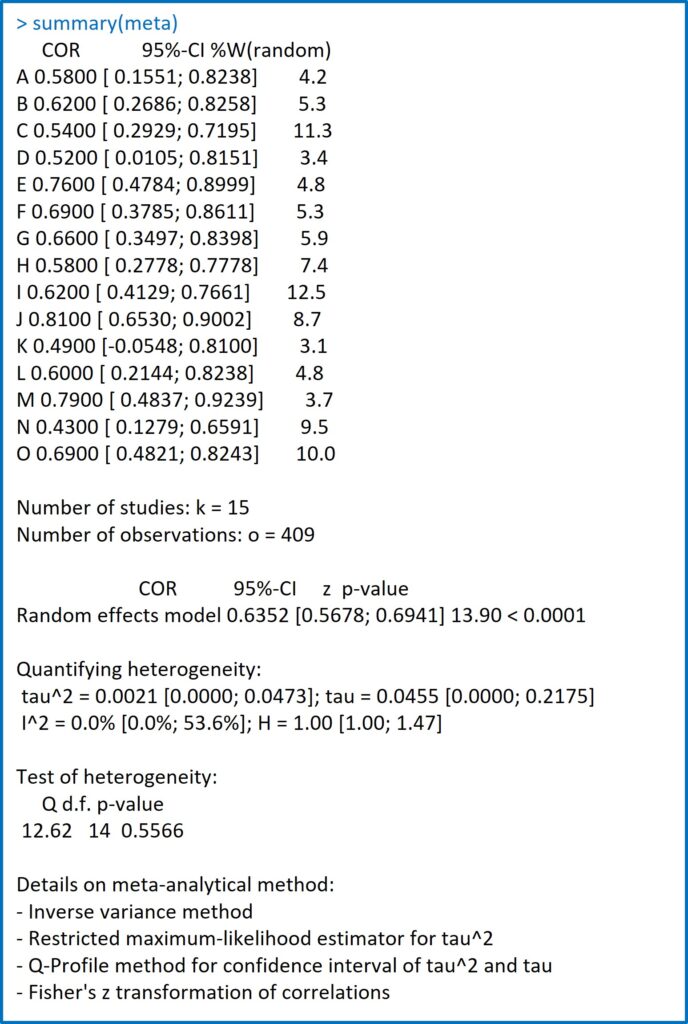
En primer lugar, nos muestra una tabla con tres columnas con el listado de estudios con sus coeficientes de Pearson (los que nosotros introdujimos), los intervalos de confianza al 95% que estima para cada uno de ellos y la ponderación que establece para cada estudio para el cálculo de la medida resumen global.
Recordad que el coeficiente R de cada estudio se considera una estimación puntual del coeficiente de la población que hace ese estudio determinado. El primer paso es calcular el intervalo de confianza, que es la estimación poblacional (de la que procede la muestra del estudio). Aquí es donde influye lo de la estabilidad de la varianza dependiente del tamaño muestral, pero si buscáis las z de Fisher no las vais a ver por ningún sitio.
Ya lo hemos comentado, el programa convierte las R en z, hace todos los cálculos y realiza la transformación inversa para enseñarnos solo valores de R, con los que solemos estar más familiarizados.
Pero las z de Fisher están en el objeto meta. Si queréis ver los valores de la z de Fisher de los estudios individuales y sus errores estándar, podéis escribir los comandos print(meta$TE) y print(meta$seTE).
Siguiendo con los resultados, después de esta tabla se muestran el número de estudios (k = 15) y de observaciones (o = 409) con los que se ha hecho el metanálisis.
El programa nos informa a continuación de que ha empleado un modelo de efectos aleatorios y ha calculado una medida global del coeficiente de correlación de Pearson de 0,63. Nos especifica su intervalo de confianza (recordemos que es una estimación del poblacional) y su significación estadística.
El resto es el estudio de heterogeneidad realizado y unas notas finales sobre la metodología del metanálisis. En la última línea nos recuerda que se ha utilizado la transformación de Fisher para estimar la medida global de correlación.
Nos vamos…
Y aquí vamos a dejar por hoy este deporte tan fatigoso del metanálisis.
Hemos visto como, de manera general, con muestras grandes el coeficiente de correlación de Pearson tiende a ser más preciso, mientras que con muestras pequeñas puede estar sujeto a mayor variabilidad y, por lo tanto, ser menos confiable como estimador de la verdadera relación entre las variables.
En estos casos, realizar la transformación de Fisher ayuda a estabilizar la varianza de las estimaciones de correlación, lo que es importante cuando se realizan inferencias estadísticas.
Un problema similar podemos encontrarlo cuando la medida global del metanálisis es una diferencia de medias de una variable cuantitativa. De forma general, es aconsejable utilizar una medida estandarizada de efecto, como la d de Cohen, pero, en casos de muestras pequeñas, también es conveniente aplicar una corrección y utilizar otro parámetro, la g de Hedges. Pero esa es otra historia…
Bibliografía
- Effect sizes. En: Harrer M, Cuijpers P, Furukawa TA, Ebert DD, eds. Doing meta-analysis with R. A hands-on guide. CRC Press. Boca Ratón, Florida, 2022;53-91. (HTML)
- Effect sizes based on correlations. En: Borenstein M, Hedges LV, Higgins JPT, Rothstein HR, eds. Introduction to meta-analysis. John Wiley & Sons. West Sussex, Reino Unido,2009; 41-9. (HTML)
- van Aert RCM. Meta-analyzing partial correlation coefficients using Fisher’s z transformation. Res Synth Methods.2023;14:768-73. (PubMed)