La polisemia de Q
La polisemia es una de las características del lenguaje, ya sabéis, esa fiesta de significados en los que una palabra decide llevar múltiples disfraces. Tomemos, por ejemplo, la letra Q.
Q es la decimoséptima letra del alfabeto latino, utilizada comúnmente en idiomas como el español, el inglés, el francés y otros muchos. Todos la conocéis, es parecida a la letra O, pero con una cola añadida que le da un toque distintivo.
De todas formas, cuando pienso en Q, mi mente deriva rápidamente al mundo del cine y las novelas de espías y me acuerdo de Q, el genio tecnológico detrás de las extravagantes aventuras de James Bond. Q es la mente maestra detrás de los gadgets más ingeniosos del MI6. Pero, seamos justos, Q no solo es el proveedor de juguetes para el agente 007, sino también el personaje que añade un toque de ingenio y astucia a la elegante y peligrosa vida de Bond.
Ya veis que Q es mucho más que una simple letra del alfabeto. Pero hoy no vamos a hablar de semántica y, mucho menos, de cine. Porque Q no es solo una letra o un apellido, es también la clave para desentrañar los misterios estadísticos que rondan nuestros metanálisis. Como un detective cuántico, otra Q, la Q de Cochran, nos ayuda a revelar la verdad oculta entre los datos, o al menos, lo intenta entre tanta incertidumbre y heterogeneidad estadística.
Pero no os preocupéis, no vamos a necesitar ni lupa ni gabardina para seguir este emocionante camino. Poneos cómodos y preparaos para pasear por un mundo donde los números hacen sus movimientos y las hipótesis se desentrañan. Vamos allá.
Una aclaración previa
Antes de empezar a hablar de cómo medir la heterogeneidad en un metanálisis, creo que merece la pena hacer una aclaración previa, porque aquí volvemos a encontrarnos con la polisemia del lenguaje y el término «heterogeneidad» puede tener dos significados.
En primer lugar, pueden existir diferencias entre los estudios primarios de un metanálisis en cuanto a población, intervención, comparación y resultados (los clásicos componentes de la pregunta clínica estructurada, PICO). Esta heterogeneidad, que podemos llamar clínica, puede reducirse cuando diseñamos nuestro estudio realizando una pregunta de investigación adecuada, pero no tiene sentido intentar corregirla en la fase de análisis de resultados.
No se deben mezclar churras con merinas. Si nos encontramos en esta situación, lo correcto es limitarnos a hacer una síntesis cualitativa de nuestra revisión sistemática y abstenernos de hacer una síntesis cuantitativa o metanálisis.
En segundo lugar, podemos encontrarnos ante lo que denominamos heterogeneidad estadística, debida a la precisión de las estimaciones que se realizan en el metanálisis. Esta heterogeneidad, que puede ser alta incluso si los estudios son muy homogéneos desde el punto de vista clínico, debe ser tenida siempre en cuenta al analizar los resultados.
La heterogeneidad estadística es la responsable de la variabilidad entre estudios del metanálisis. Porque, una vez más, podemos encontrar también más de una fuente de variabilidad.
Fuentes de variabilidad en el metanálisis
A la hora de considerar las fuentes de variación entre los efectos observados en los estudios primarios del metanálisis, podemos utilizar dos modelos diferentes: el modelo de efecto fijo y el modelo de efectos aleatorios.
El modelo de efecto fijo asume que el efecto que queremos estimar es el mismo en las poblaciones de las que proceden las muestras con las que se realizan los estudios primarios. De esta forma, las diferencias observadas entre los efectos de los estudios son debidas únicamente al azar.
Por su parte, el modelo de efectos aleatorios supone que cada población tiene su efecto específico, de forma que estos efectos aleatorios se consideran variables aleatorias que siguen una distribución determinada, y su inclusión en el modelo ayuda a mejorar la precisión de las estimaciones y a tener en cuenta la variabilidad entre los estudios.
Así, las fuentes de variabilidad son dos bajo el modelo de efectos aleatorios. Por una parte, nuestro compañero inseparable, el azar. Por otra, la variabilidad entre estudios. Y aquí entra en juego la Q de Cochran, que nos ayuda a diferenciar entre el error aleatorio o de muestreo y el debido a diferencias reales entre los diferentes estudios del metanálisis.
La Q de Cochran
Allá por los años 50 del siglo pasado, Cochran definió su famosa Q recurriendo a una herramienta muy querida en el mundo de la estadística, que no es otra que la suma de los cuadrados de las diferencias entre el valor observado y el calculado: los residuos. En este caso, se calcula la suma de los cuadrados de las diferencias entre el efecto de cada estudio y la medida de efecto resumen calculada según el modelo de efecto fijo, ponderando cada diferencia por el peso de cada estudio.
Como una imagen vale más que mil palabras (o eso dicen), os muestro la fórmula a continuación.
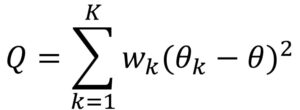
Vamos a fijarnos un poco más en la fórmula, aunque a muchos les apetecería más olvidarla cuanto antes. La letra θ representa la medida de efecto resumen calculada aplicando, como ya hemos dicho, un modelo de efecto fijo, mientras que θk representa el efecto de cada estudio primario. K representa el número de estudios, siendo k cada estudio individual. Por último, wk es el peso de cada estudio, calculado como el inverso de su varianza (lo habitual en el modelo de efecto fijo).
Podemos comprender con facilidad que el valor de Q aumentará al hacerlo el número de estudios. Además, al ponderarse por el inverso de la varianza (el error estándar del efecto), los estudios con un error muy pequeño influirán mucho en el valor de Q, aunque el valor del efecto se diferencie poco de la medida resumen.
El valor obtenido de Q puede utilizarse para medir el exceso de variación que podemos atribuir exclusivamente al azar o, lo que es lo mismo, la heterogeneidad entre estudios. Pero, ¿qué valor de Q nos indicará que existe heterogeneidad más allá de la explicada por error de muestreo?
La respuesta es que no hay un valor que podamos establecer de forma general, sino que dependerá de cada caso, así que, para comprender mejor cómo calcularlo, vamos a hacer una pequeña simulación con datos totalmente inventados.
Experimentando con la Q de Cochran
Vamos a ver cómo se comporta el valor de Q bajo los supuestos de ausencia y presencia de heterogeneidad. Para ello, vamos a utilizar el programa R para calcular la distribución que siguen los valores de Q en estas dos situaciones. Iré escribiendo los comandos de R, por si alguien quiere replicar el experimento al mismo tiempo que lo vamos realizando.
Ausencia de heterogeneidad
Empecemos asumiendo que no existe heterogeneidad. Esto implica que el valor de los residuos (la diferencia entre el efecto de cada estudio y la medida resumen con el modelo de efecto fijo) se distribuye de forma normal alrededor del valor de la medida resumen, con una media de 0 y una determinada varianza que, en este caso, vamos a suponer que es 1. Así, podemos decir que los residuos se distribuyen según una normal estándar N(0,1).
Suponiendo que nuestro metanálisis tenga 35 estudios, podríamos calcular los valores de los residuos con la función rnorm() de R:
residuos <- rnorm(n = 35, mean = 0, sd = 1)
Esto nos daría los valores de los residuos para nuestro metanálisis, pero lo que nos interesa es saber cómo se comportan estos residuos si repetimos muchas veces el estudio, para poder calcular la distribución muestral de los residuos y, a partir de ella, la de Q. Podemos simular que repetimos el metanálisis 10000 veces con el siguiente comando:
err_fijo <- replicate(10000, rnorm(n = 35, mean = 0, sd = 1))
Por último, recordando la fórmula de Q, podemos calcular su valor en cada uno de estos 10000 metanálisis. Para simplificar, vamos a suponer que el peso de todos los estudios es igual a 1:
Q_fijo <- replicate(10000, sum(rnorm(n = 35, mean = 0, sd = 1) ^ 2))
Que nadie se preocupe en exceso si no entiende bien cómo hacemos la simulación. Lo interesante viene ahora.
Como es una suma ponderada de cuadrados, Q solo puede adquirir valores positivos, y sabemos que sigue, aproximadamente, una distribución de la ji-cuadrado con un número de grados de libertad igual al número de estudios menos uno (K – 1). Aprovecho para recordar que la distribución de la ji-cuadrado se caracteriza por tener una media igual al número de grados de libertad y una varianza igual al doble de los grados de libertad.
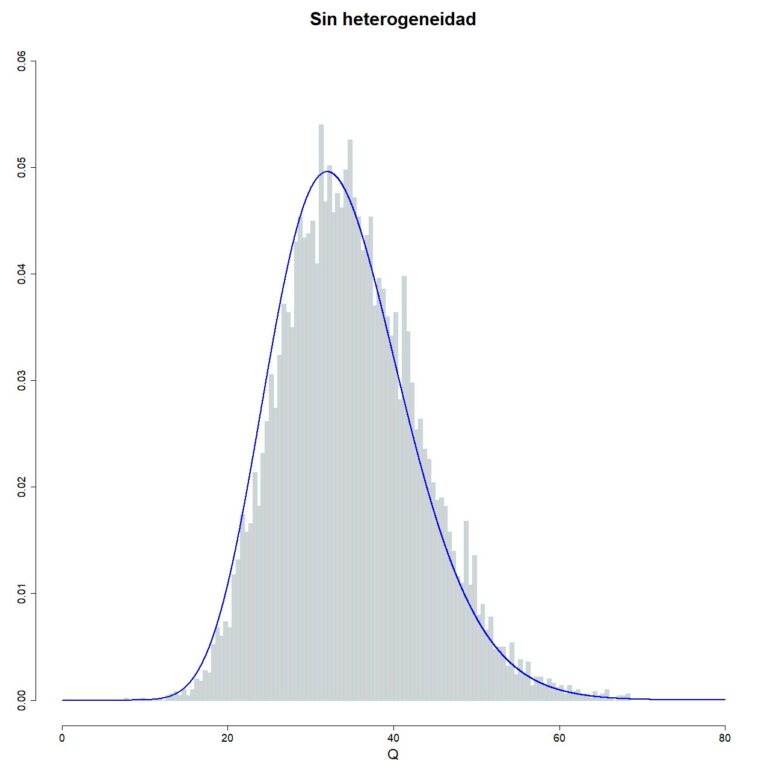
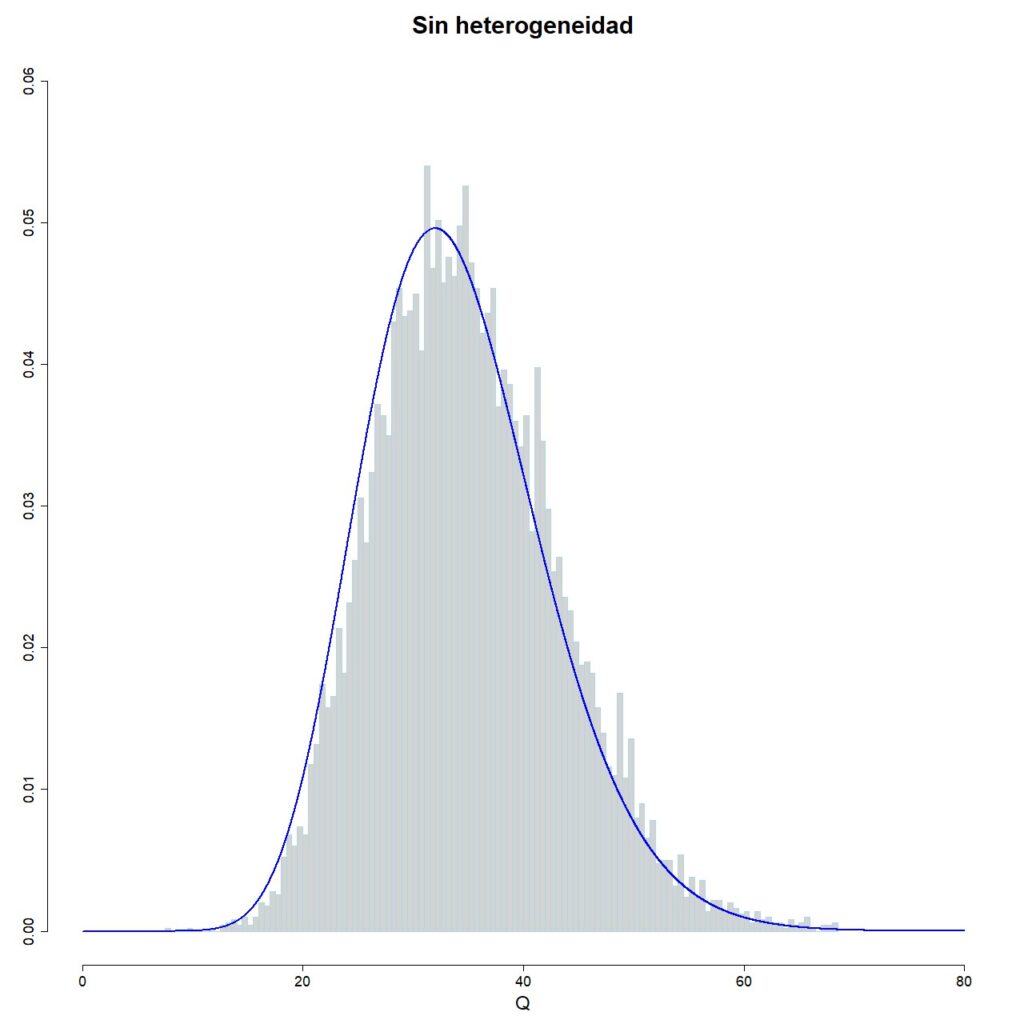
Para comprobar que nuestra simulación funciona, representamos el histograma de la distribución muestral de Q, superponiendo la curva de la distribución de la ji-cuadrado con 35-1 grados de libertad:
hist(Q_fijo, xlab=»Q», prob = TRUE, breaks = 100, ylim = c(0, 0.06), xlim = c(0, 80), ylab = «»,
main = «Sin heterogeneidad», border=»lightblue»)
lines(seq(0, 80, 0.01), dchisq(seq(0, 80, 0.01), df = 35-1), col = «blue», lwd = 2)
Como podéis ver en la figura 1, los datos de Q de los 10000 estudios simulados siguen, de forma razonable, la distribución, así que no hay sorpresas hasta ahora.
Presencia de heterogeneidad
En este caso, tenemos que asumir que los residuos tienen dos componentes de variabilidad: el azar y la variabilidad entre estudios. Podemos calcularlo de forma similar a como hicimos antes, pero sumando este segundo componente:
residuos <- rnorm(n = 35, mean = 0, sd = 1) + rnorm(n = 35, mean = 0, sd = 1)
Ahora calculamos los valores de Q para los 10000 metanálisis simulados bajo el supuesto de que existe heterogeneidad:
Q_alea <- replicate(10000, sum((rnorm(n = 35, mean = 0, sd = 1) +
rnorm(n = 35, mean = 0, sd = 1))^2))
Ya solo nos queda hacer la representación gráfica, de forma similar a como hicimos antes:
hist(Q_alea, xlab=»Q», prob = TRUE, breaks = 100, ylim = c(0, 0.06), xlim = c(0, 160), ylab = «»,
main = «Con heterogeneidad», border = «pink»)
lines(seq(0, 100, 0.01), dchisq(seq(0, 100, 0.01), df = 35-1), col = «red», lwd = 2)
El resultado se muestra en la figura 2.
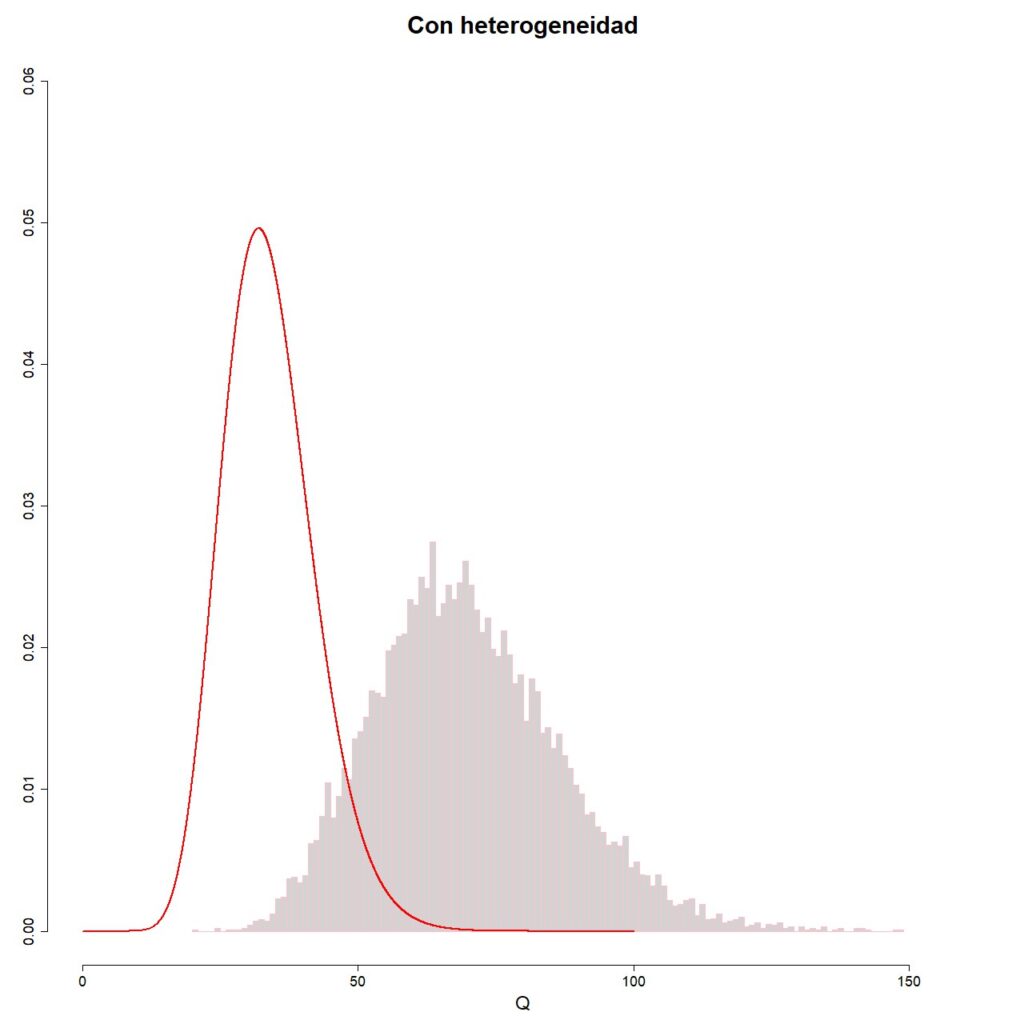
Como podéis ver, esta vez la distribución muestral de los valores de Q no se ajusta a la teórica distribución de la ji-cuadrado. Para ello, debería cumplirse el supuesto de no heterogeneidad que, como sabemos, no se cumple en esta ocasión.
Pues bien, es esta desviación de la distribución teórica, cuando existe variabilidad entre estudios, la que podemos utilizar para determinar si hay heterogeneidad entre los estudios primarios.
El contraste de hipótesis para la Q de Cochran
Vamos a realizar un contraste de hipótesis bajo el supuesto de que se cumple la hipótesis nula de ausencia de heterogeneidad.
Lo que hacemos es calcular el valor de la Q de Cochran con los efectos de los estudios de nuestro metanálisis. Idealmente, bajo el supuesto de la hipótesis nula, el valor esperado es K-1 (la media de la distribución), aunque ya sabemos que el valor será casi siempre diferente, aunque solo sea por error aleatorio.
Solo nos quedará calcular la probabilidad de encontrar un valor de Q tan extremo o más que el que hemos encontrado, solo por azar. Si esta probabilidad (el valor p) es mayor de 0.05, no podremos rechazar la hipótesis nula y asumiremos que no existe heterogeneidad.
Por el contrario, si p < 0.05, rechazaremos la hipótesis y concluiremos que existe heterogeneidad estadística entre los estudios primarios del metanálisis.
Veamos un ejemplo. Supongamos que en nuestro metanálisis de 35 estudios hemos calculado el valor de la Q de Cochran, que es igual a 52.5. Para obtener el valor de p, podemos ejecutar en R el siguiente comando:
pchisq(q = 52.5, df = 34, lower.tail = FALSE)
Este comando nos proporciona la probabilidad de obtener, solo por azar, un valor de Q como el que hemos obtenido o mayor (el área bajo la curva de la cola derecha). El programa nos da un valor de p = 0.02. Podemos rechazar la hipótesis nula y concluir que existe heterogeneidad entre los estudios primarios.
Como siempre, lo importante es entender el concepto. De todos estos cálculos se encargará el programa de estadística con el que realicemos el metanálisis.
Variaciones sobre un tema de Cochran
La Q de Cochran es una medida muy utilizada para detectar la heterogeneidad y, de una manera aproximada, podemos decir que será mayor cuanto mayor sea la variabilidad entre estudios.
El problema es que su valor resulta poco intuitivo para valorar la intensidad de esta variabilidad, por lo que se han desarrollado dos estimadores más, que pretenden ser más sencillos de interpretar. Estos son la I2 y la H2, que pueden calcularse a partir del valor de Q.
El estadístico I2
La I2 define el porcentaje de variabilidad del tamaño de los efectos que no está causado por error aleatorio o, lo que es lo mismo, el debido a heterogeneidad. Se calcula según la siguiente fórmula.
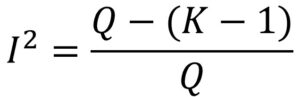
Ya sabemos que, si no existe heterogeneidad, el valor esperado de Q es K-1 (la media de la distribución de la ji-cuadrado). Si al valor de Q (observado) le restamos K-1 (el valor esperado debido a error aleatorio) y lo dividimos por el total de Q, nos dará la proporción del valor de Q que no se explica por azar.
En el caso de que Q sea menor que la media esperada (K-1), asumimos que I2, que suele multiplicarse por 100 y expresarse como porcentaje, vale 0 (es lógico, la proporción de variabilidad debida a heterogeneidad podrá ser más o menos elevada, pero nunca menor de 0%).
El valor de I2 puede oscilar de 0 a 100%, considerándose habitualmente los límites de 25%, 50% y 75% para delimitar cuando existe una heterogeneidad baja, moderada y alta, respectivamente.
Una ventaja de la I2 es que no depende de las unidades de medida de los efectos ni del número de estudios, por lo que, a diferencia de lo que ocurre con la Q, sí permite comparaciones con distintas medidas de efecto y entre diferentes metanálisis con diferente número de estudios.
Si calculamos el valor de I2 en nuestro ejemplo con 35 estudios y un valor de Q de 52.5, vemos que es del 35.2%, lo que indica una heterogeneidad moderada.
El estadístico H2
Este estadístico, mucho menos famoso que el anterior, se calcula también a partir del valor de Q y representa la razón entre el valor observado (Q) y el esperado bajo el supuesto de la hipótesis nula (K-1, la media de la distribución):
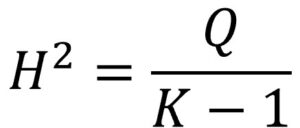
En este caso no es necesario hacer ninguna corrección cuando el valor de Q es menor de K-1. Cuando no existe heterogeneidad H2 ≤ 1. Los valores mayores de 1 indican variabilidad entre los estudios.
En nuestro ejemplo, con un valor de Q de 52.5 y 35 estudios, H2 vale 1.54, lo que indica la existencia de heterogeneidad.
Nos vamos…
Y hasta aquí hemos llegado en el día de hoy.
Hemos visto como se suele utilizar el valor de la Q de Cochran para detectar la heterogeneidad entre los estudios de un metanálisis, a pesar de que tiene algunos defectos, como el depender del número y la precisión de los estudios.
La I2, por su parte, es algo menos sensible a estos efectos y más fácil de interpretar, pero sigue dependiendo de la precisión de los estudios incluidos en el metanálisis. Si los estudios tienen muestras muy grandes, el error aleatorio tenderá a 0, pero Q aumentará al ponderarse por el inverso de la varianza y el valor de I2 tenderá hacia el 100%.
Por eso no es buena idea limitarse a calcular los valores de Q y de I2 (o de H2, que se comporta de forma similar a I2) y muchos autores aconsejan completar la valoración de la heterogeneidad con el cálculo de la τ2 (que no es, en sentido estricto, una medida de heterogeneidad) y de intervalos de predicción. Pero esa es otra historia…
BIBLIOGRAFÍA.
- Between-study heterogeneity. En: Harrer M, Cuijpers P, Furukawa TA, Ebert DD, eds. Doing meta-analysis with R. A hands-on guide. CRC Press. Boca Ratón, Florida, 2022;139-71. (HTML)
- Identifying and quantifying heterogeneity. En: Borenstein M, Hedges LV, Higgins JPT, Rothstein HR, eds. Introduction to meta-analysis. John Wiley & Sons. West Sussex, Reino Unido,2009; 107-26. (HTML)