Molina Arias, M
Servicio de Gastroenterología. Hospital Infantil Universitario La Paz. Madrid. España.
Un error que los clínicos cometemos con más frecuencia de la deseable es interpretar el resultado de una prueba diagnóstica como un veredicto definitivo: el paciente está enfermo o está sano, ¿no es verdad?
Pero hoy os voy a contar un pequeño secreto del mundo de la medicina: la realidad rara vez es tan simple. Cuando tratamos con pruebas diagnósticas, nos sumergimos en un intrincado juego de probabilidades en el que no existe una línea divisoria nítida. Esto es especialmente así cuando tenemos que elegir el punto de corte de una prueba con un resultado continuo o, en el caso de una prueba con resultado dicotómico (positivo o negativo), cuando tenemos que elegir el punto de corte en el modelo que nos proporciona la probabilidad de que el paciente esté o no enfermo.
El problema en muchos casos es que, sea cual sea el punto elegido, no podremos aprovechar al máximo todas las cualidades de la prueba. Al igual que en otros muchos aspectos de la vida, donde debemos hacer elecciones y renuncias, en el mundo de las pruebas de diagnóstico la elección del punto de corte perfecto se convierte en un arte en sí mismo en el que, en lugar de buscar la respuesta definitiva, nos encontraremos buscando el delicado equilibrio entre la precisión y la sensibilidad de la prueba.
Pero que nadie desespere por este comienzo tan pesimista. Existen herramientas que nos ayudan a educar el arte de la renuncia y nos permiten elegir, si no un punto ideal, sí el más adecuado a cada situación. De una de estas herramientas vamos a hablar hoy. Es otro de esos recursos que vienen del mundo de la ciencia de datos y que tiene el deslumbrante nombre de razón de enriquecimiento de la precisión respecto a la prevalencia.
Veamos de qué va todo esto.
Planteamiento del problema
Para mostrar de manera más sencilla el problema de la elección del punto de corte, veremos un par de ejemplos en los que elaboraremos un modelo de regresión logística múltiple para estimar la probabilidad de enfermedad en función de los valores de varias variables independientes que podemos obtener del paciente.
Una vez elaborado el modelo, aplicado a cada paciente, nos proporcionará el logaritmo de la odds ratio de que el paciente presente el resultado definido como 1 en la variable dependiente binaria (0 = sano, 1 = enfermo, lo más habitual). A partir de este resultado podemos calcular la probabilidad de que esté enfermo o, lo que es lo mismo, de que el valor de la variable dependiente sea 1.
En la práctica, un valor de probabilidad aislado resulta poco útil, por lo que tendremos que elegir un punto de corte por encima del cual consideraremos que el resultado de la prueba es positivo (está enfermo) y por debajo, que es negativo (está sano). Finalmente, este resultado, positivo o negativo, se comparará con el obtenido con el del patrón de referencia, que asumimos nos dice con seguridad si el paciente está sano o enfermo.
Esta comparación se hace con la habitual tabla de contingencia, que nos permite calcular parámetros como sensibilidad (S), especificidad (E), valores predictivos y cocientes de probabilidad. En general, solemos basarnos fundamentalmente en dos parámetros para valorar cuál es el punto de corte adecuado a nuestro escenario clínico.
El primero es la S, la proporción de enfermos en los que se obtendrá un resultado positivo con la prueba. El segundo es la precisión de la prueba, que nos dice qué proporción de los positivos son realmente enfermos. Es lo que los clínicos conocemos mejor como valor predictivo positivo (VPP).
La pregunta del millón es, en cada caso, qué punto de corte de probabilidad elegimos. Una respuesta rápida, sobre todo si usamos un modelo de regresión logística, sería elegir el de la probabilidad mayor o igual a 0.5 para el resultado positivo y la de menos de 0.5 para el resultado negativo, que sería el punto de corte «natural» para la función logística del modelo. Como es fácil de imaginar, esto funcionará muy pocas veces, generalmente cuando la prevalencia de la enfermedad esté próxima a 0.5.
Otra cosa que podemos hacer es representar gráficamente las probabilidades obtenidas en los dos grupos (sanos y enfermos según el patrón de referencia). En un mundo ideal, las dos curvas de densidad de probabilidad estarían más o menos bien diferenciadas, con lo que nos iríamos al valle central donde los valores de las dos curvas son mínimos. A la derecha estarían los positivos y, a la izquierda, los negativos.
Pero en nuestra realidad cotidiana, las cosas no suelen ser tan sencillas. Vamos con un par de ejemplos para entenderlo mejor.
Ejemplo práctico (relativamente sencillo)
Para ilustrar los ejemplos, voy a utilizar el programa R, de acceso libre. Si queréis reproducir el experimento tal cómo se va relatando en esta entrada, podéis bajaros el script de este enlace.
Para este primer supuesto, voy a utilizar el conjunto de datos Pima.te, del paquete MASS de R. Contiene un registro de 332 mujeres gestantes mayores de 21 años que son evaluadas para un diagnóstico de diabetes gestacional según los criterios de la OMS. Además del diagnóstico de diabetes (sí/no), contiene información sobre el número de gestaciones, glucemia plasmática, presión arterial sistólica, pliegue tricipital, índice de masa corporal, antecedente de diabetes y edad.
En este conjunto de datos hay 109 diabéticas y 223 no diabéticas, lo que supone una prevalencia de diabetes gestacional de 0.33.
En este caso, vamos a elaborar un modelo de regresión logística múltiple con el diagnóstico de diabetes (1 = sí, 0 = no) como variable dependiente y la glucemia y el índice de masa corporal como variables independientes. No vamos a preguntarnos si este es el mejor modelo posible, ya que no es el tema de esta entrada y, tal como lo hemos descrito, nos sirve perfectamente para lo que queremos demostrar.
Antes de elegir un punto corte para considerar el resultado de la prueba (el modelo) como positivo o negativo, podemos estimar su desempeño global calculando el área bajo la curva ROC (ABC), que podéis ver en la figura 1. Nuestro cálculo nos dice que la prueba tiene un ABC = 0,82, lo que nos sugiere que tiene un buen desempeño en la discriminación entre resultados positivos y negativos.
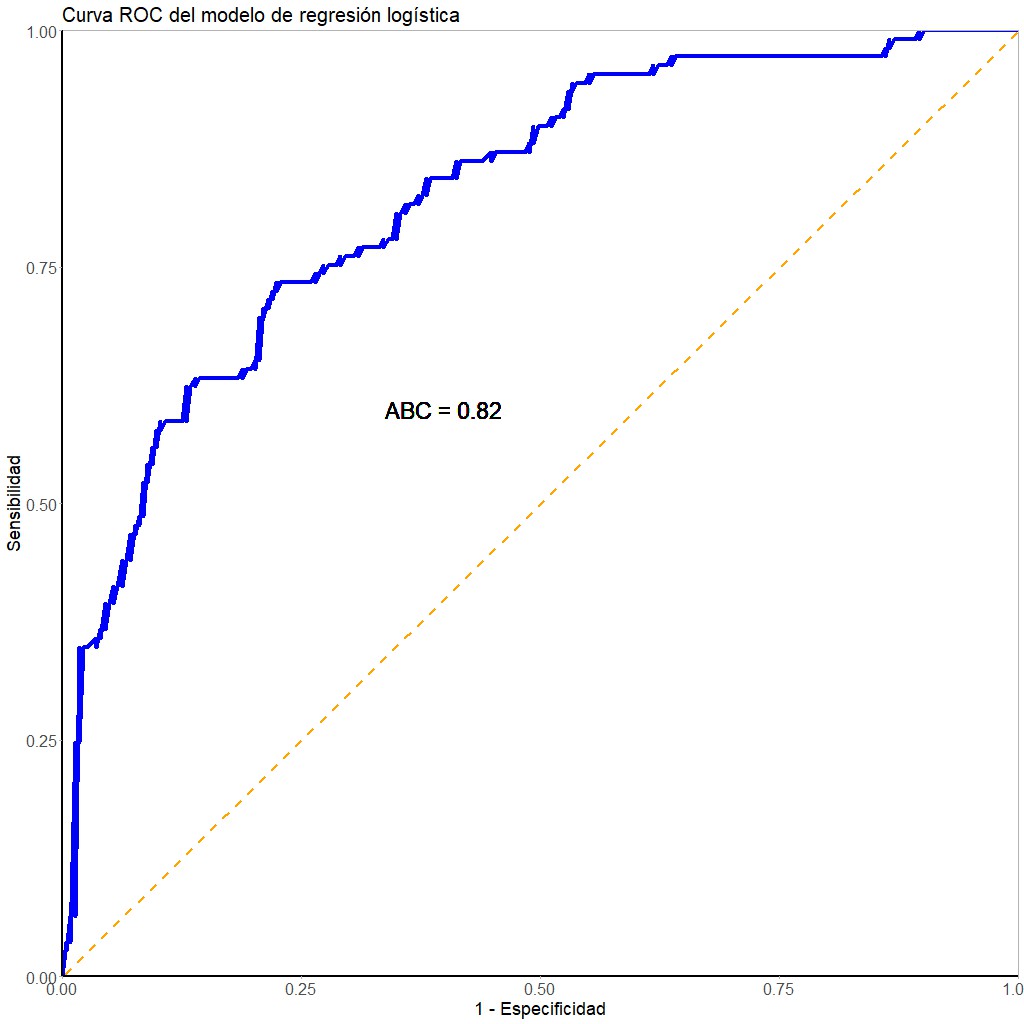
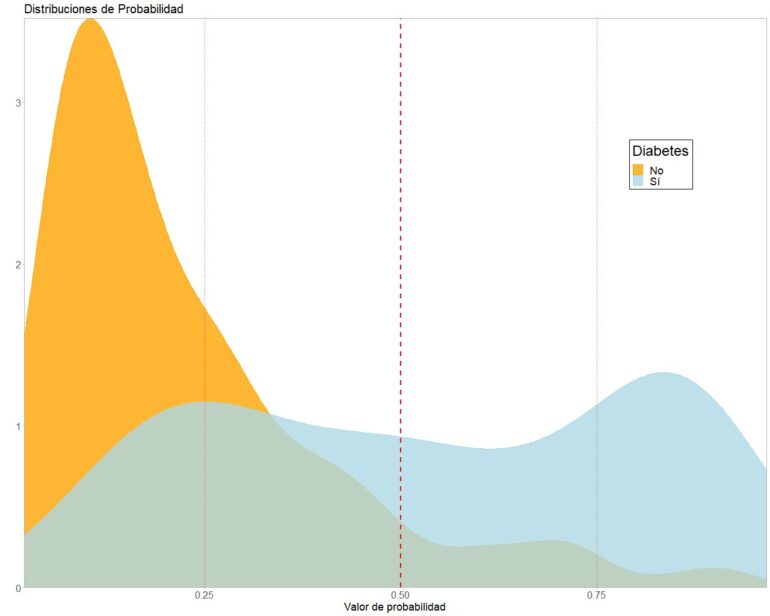
Ahora nos toca elegir el punto de corte de la prueba. Para ello, empezamos por representar gráficamente las funciones de densidad de las probabilidades que nos da el modelo para los dos grupos, como veis en la figura 2.
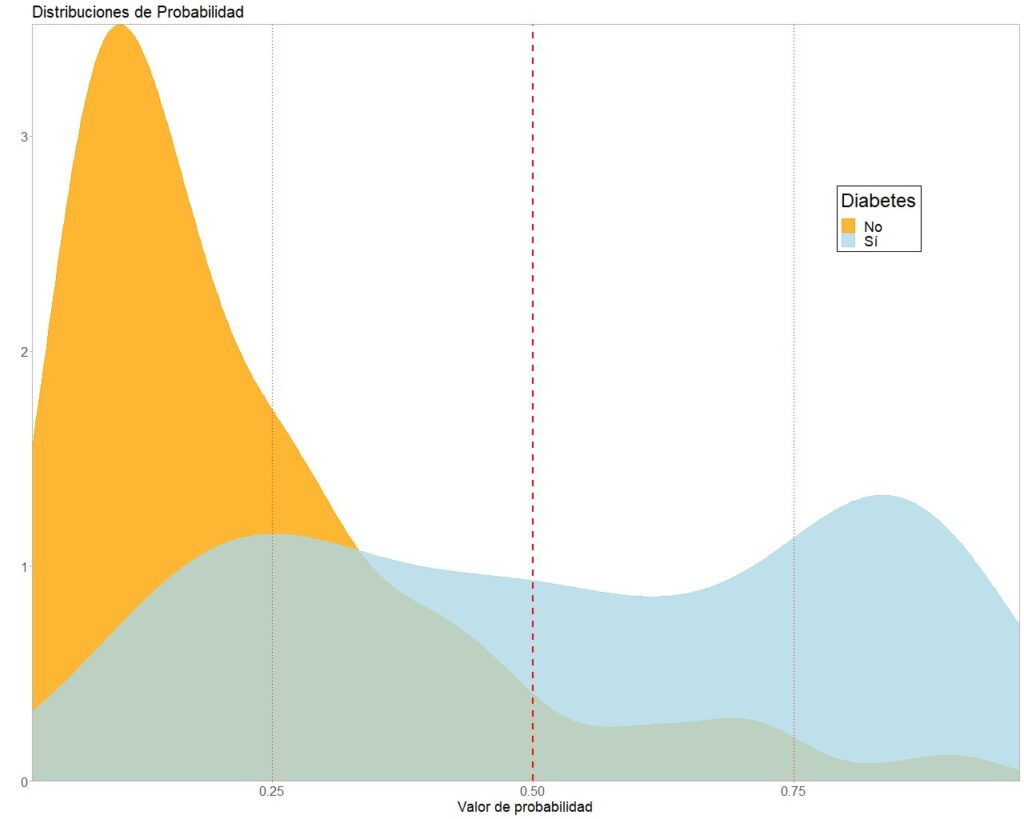
Como ocurre con frecuencia en la vida real, hay bastante solapamiento entre las dos curvas, con lo que ningún punto de corte nos va a separar perfectamente las enfermas de las sanas.
Vamos a empezar a educar nuestro arte de la renuncia valorando, como punto de corte, el correspondiente a la probabilidad de 0.5, marcado con la línea roja discontinua.
Podemos calcular que, para este punto de corte, la S = 0.53 y la E = 0.91. El rendimiento para las gestantes no diabéticas parece adecuado, ya que solo 20 de las 223 serían diagnosticadas como diabéticas por error (falsos positivos, FP). Sin embargo, dejaríamos sin diagnosticar 73 diabéticas, todas aquellas cuya probabilidad está a la izquierda del punto de corte.
¿Cómo podemos optimizar esta elección? Si nos vamos hacia la derecha, aumentarán la E y el VPP de la prueba, pero disminuirá aún más la S. En el punto de corte p = 0.75, tendremos una S = 0.33, una E = 0.98 y un VPP = 0.9.
Por el contrario, si nos vamos hacia la izquierda, la S aumentará, pero también lo harán los FP al disminuir la E y el VPP. Para p = 0.25, la S = 0.77, la E = 0.66 y el VPP = 0.53. Podéis ver cómo cambian estos parámetros para diferentes puntos de corte en la figura 3.
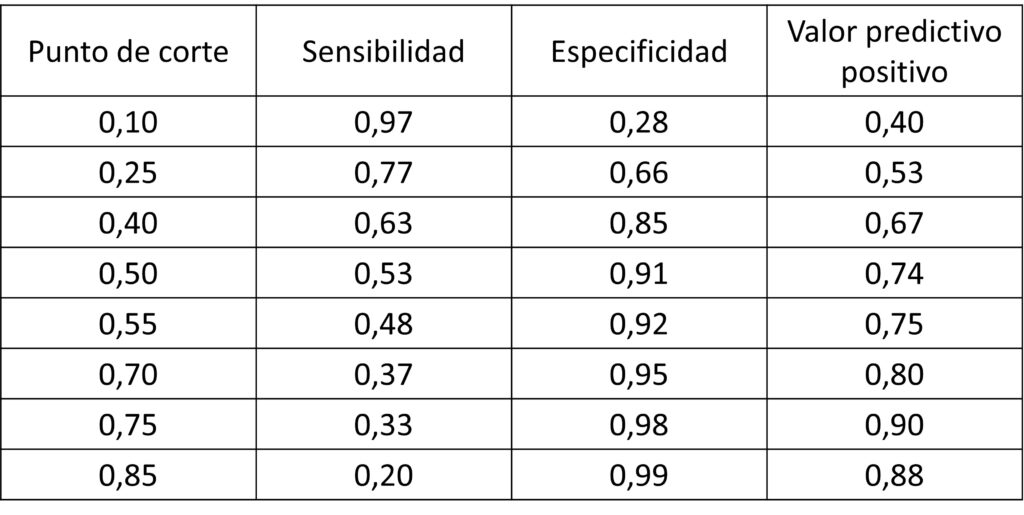
Vemos, pues, que no es posible tener muy buena S y E al mismo tiempo, hay que priorizar una de las dos. Tendremos que decidir si queremos favorecer la S (irnos hacia la izquierda de la curva) o la precisión de la prueba, reflejada por su E y su VPP (movernos hacia la derecha). De todas formas, en este ejemplo no tendríamos que hacer una renuncia excesiva, ya que no hay gran variación entre los indicadores, salvo que nos vayamos a los extremos de los valores de probabilidad generados por el modelo diagnóstico.
Teniendo en cuenta el contexto clínico, probablemente elijamos priorizar más la sensibilidad que la precisión. Seguramente preferiremos que se quede sin diagnosticar el menor número posible de gestantes diabéticas. El precio que habrá que pagar será un mayor número de falsos positivos, pero que podremos diagnosticar de forma correcta posteriormente con otra prueba relativamente sencilla, como una sobrecarga de glucosa. En mi opinión, un buen punto de corte para este modelo estaría entre 0.2 y 0.3.
Otro ejemplo práctico (algo más complejo)
Vamos a ver ahora otro escenario clínico algo más complejo de resolver. Para ello, recurrimos a un conjunto de datos que me acabo de inventar y que incluye los resultados de un estudio ficticio para el diagnóstico de esa terrible enfermedad que es la fildulastrosis. Podéis descargar los datos en este enlace.
Se trata de un registro de 10.000 pacientes que acuden a un servicio de Urgencias y en el que se recogen datos de la determinación de algunas moléculas que pueden ayudar al diagnóstico de esta enfermedad, como son el cafresterol, la vitaminita, el endorfinol, la idiotina, la estupidina y la lipidosina. Completa el registro el diagnóstico de fildulastrosis (0 = no, 1 = sí) según resultado de la fildulastrina magnética, el patrón de referencia para esta enfermedad.
En este conjunto de datos hay 473 pacientes con fildulastrosis, lo que supone una prevalencia para la enfermedad de 0.047, redondeando, un 5%.
Para empezar a resolver el problema, elaboramos un modelo de regresión logística múltiple con el diagnóstico de fildulastrosis (1 = sí, 0 = no) como variable dependiente y el resto de las determinaciones analíticas como variables independientes. Como en el caso anterior, no vamos a preguntarnos si este es el mejor modelo posible, no es el tema que nos toca hoy.
También como en el ejemplo anterior, nos fijaremos primero en el desempeño global del modelo (figura 4). Vemos que tiene un ABC = 0.87, lo que sugiere que la prueba (el modelo) tiene buena capacidad para discriminar entre sanos y enfermos.
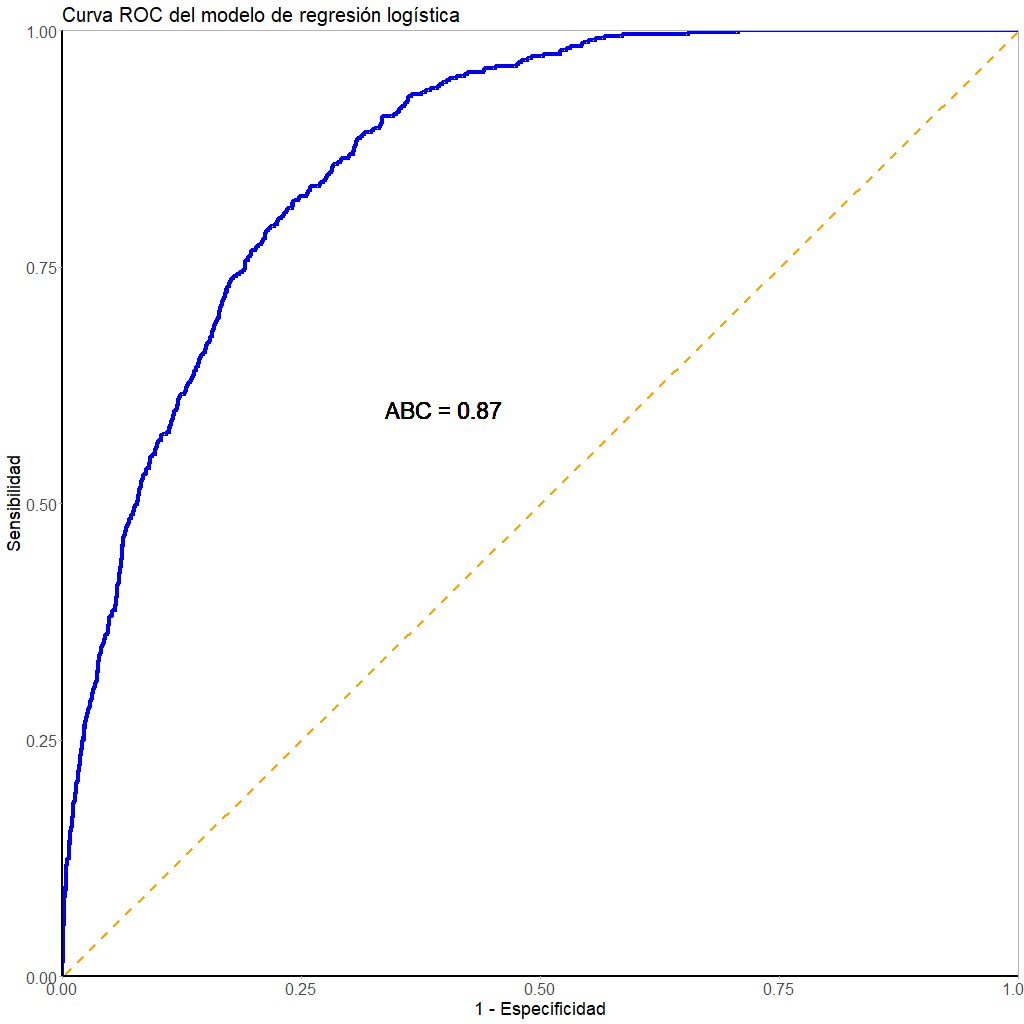
Este es un buen comienzo, así que nos animamos bastante. Parece que, una vez aprendido el procedimiento con el ejemplo de las gestantes diabéticas, resolver este escenario va a ser pan comido.
Sin embargo, la euforia se desvanece con rapidez cuando vemos las curvas de densidad de probabilidades que el modelo proporciona para los dos grupos (figura 5). Lo que vemos ahora ya no es simplemente solapamiento de las dos curvas, sino que se parece más a una superposición. ¿Cómo vamos a diferenciar entre sanos y enfermos?
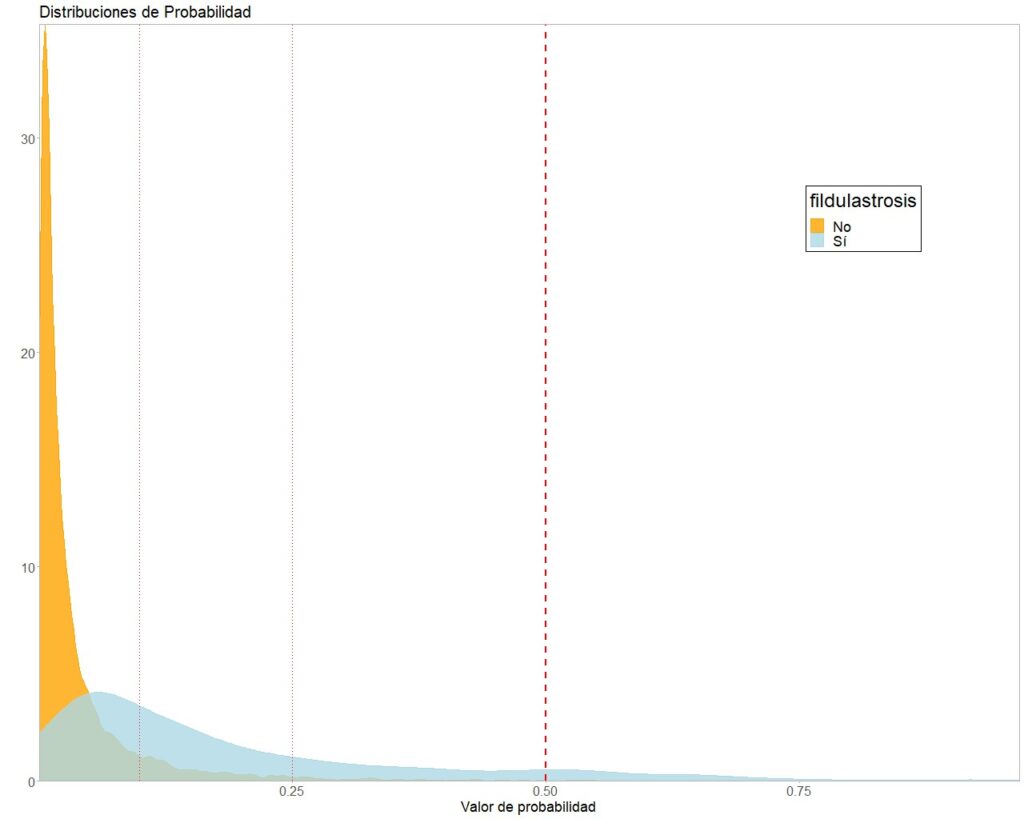
En este escenario tiene poco sentido elegir el punto de corte p = 0.5. Tendríamos una E muy alta, con muy pocos falsos positivos, pero la S sería demasiado baja, de 0.09, con lo que dejaríamos sin diagnosticar a 400 de los 473 pacientes. En una palabra: desastroso.
No tenemos más remedio que movernos, y bastante, hacia la parte izquierda de la curva. Podéis ver el rendimiento de la prueba para distintos puntos de corte en la figura 6.
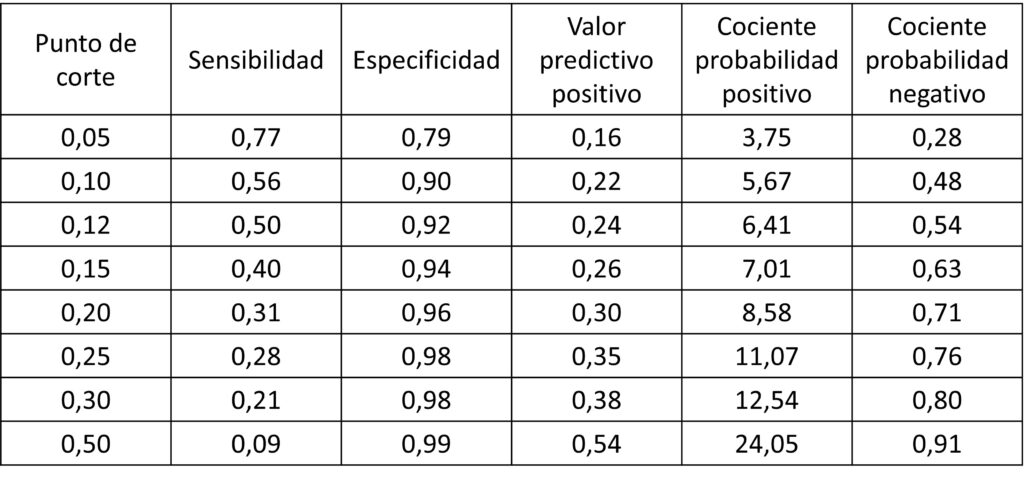
Para p = 0.25, obtenemos S = 0.25 y VPP = 0.35. Todavía nos dejamos sin diagnosticar 352 pacientes, a pesar de tener 220 FP. En otra palabra: otro desastre (bueno, en dos palabras).
Vencidos por el desánimo, nos vamos tan al extremo como p = 0.05. Como es lógico, ha mejorado la sensibilidad, 0.77, pero la precisión sigue siendo muy baja, con un VPP = 0.15. Esto implica cerca de 2000 FP, en los que tendríamos que descartar la enfermedad haciendo una fildulastrina magnética, una prueba tremendamente cara y molesta para el paciente.
¿Qué podemos hacer? ¿Hay alguna solución a este problema?
Pues sí, la hay. Pero esta solución necesita que utilicemos dos recursos. El primero, que pongamos en marcha nuestro arte de la renuncia. El segundo, el empleo de otra herramienta: la razón de enriquecimiento.
Razón de enriquecimiento de la precisión
Cuando tratamos con enfermedades con baja prevalencia podemos vernos con frecuencia en una situación similar a la presente. Hay casi solapamiento de las curvas de densidad, lo que dificulta enormemente elegir un punto de corte.
En estos casos, podemos aprovechar la ventaja que nos aporta el hecho de que la curva de probabilidad disminuya antes en los negativos que en los positivos. Esto significa que, según nos movemos hacia la derecha desde el extremo más bajo de probabilidad, el modelo irá identificando subpoblaciones en los que el riesgo de estar enfermos es mayor que en el conjunto global de pacientes (es lógico, lo vemos por el aumento del VPP).
No podremos utilizar la prueba para clasificar sanos y enfermos con buena sensibilidad y precisión, pero sí que podemos identificar sujetos cuyo riesgo de estar enfermos sea mayor que la media. De esta forma, nos moveremos hacia la derecha observando cuidadosamente cuánto disminuye la S y cuánto aumenta la precisión (el VPP) respecto a la prevalencia de la enfermedad. Este cociente entre VPP y prevalencia es lo que se conoce como razón de enriquecimiento.
Podemos representarlo gráficamente, tal como aparece en la figura 7.
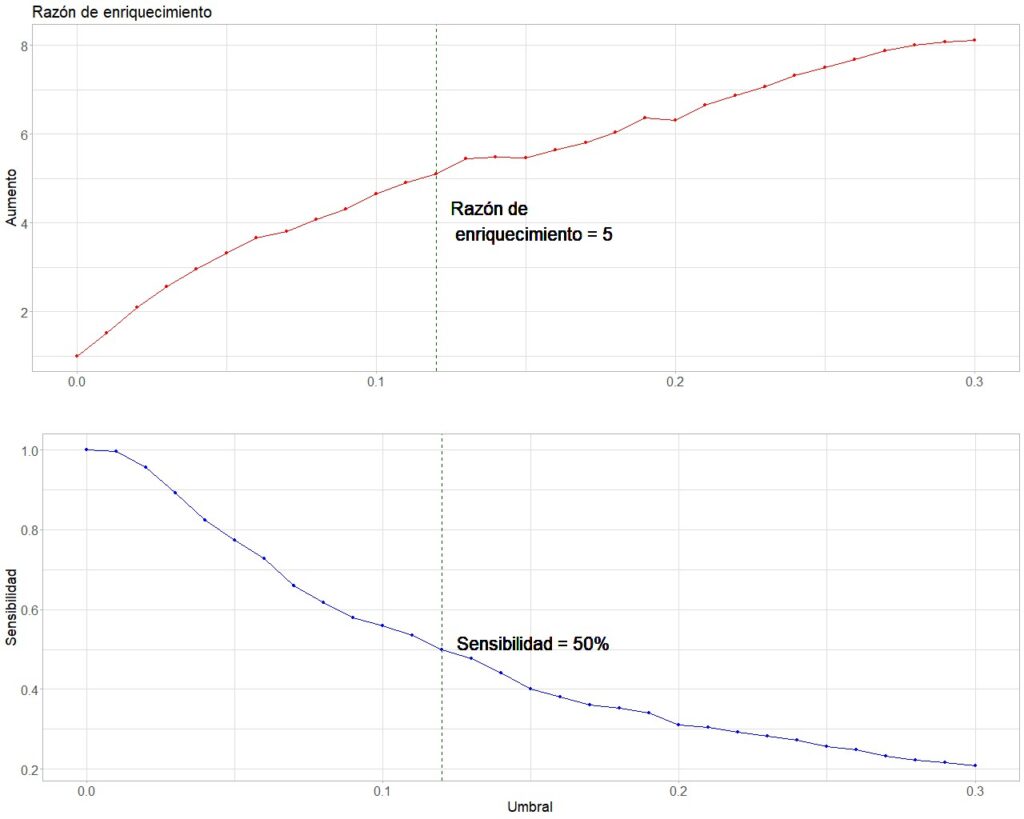
En el gráfico inferior observamos la evolución de los valores de S al aumentar el umbral de probabilidad que consideramos como punto de corte. Como ya sabemos, cuanto mayor sea este umbral de probabilidad, menor S tendrá la prueba.
En el gráfico superior vemos cómo aumenta la razón de enriquecimiento al movernos hacia la derecha. Esto es lógico, ya que esta razón es directamente proporcional a la precisión de la prueba y, por tanto, a su VPP.
Finalmente, podemos trazar una línea en el punto en el que consideremos que no podemos perder más sensibilidad y que, a la vez, nos permita detectar los individuos con un riesgo un número de veces mayor que la media adecuado a nuestro escenario.
En este ejemplo ficticio, a mí me parece correcto elegir un umbral p = 0.12. Ya he utilizado la nueva herramienta. Ahora toca ejercitar el arte de la renuncia. En este punto de corte tengo una S = 0.5, lo que significa que solo diagnostico a la mitad. El resto tendrá que esperar a presentar más síntomas de enfermedad para que tratemos de descartarla por otros medios, que seguramente serán más caros y molestos. A cambio, detecto una población con un riesgo de enfermedad cinco veces superior a la media, o sea, con una probabilidad de 0.25, aproximadamente. A estos habrá que hacerles la fildulastrina magnética, que solo será positiva en uno de cada cuatro.
Una reflexión
Supongo que, a estas alturas, mucho estaréis pensando que la prueba no vale para nada. Además, algunos os preguntaréis como una prueba tan poco útil puede tener unos indicadores de desempeño tan buenos. Si recordáis, el ABC = 0.87.
El problema es que la potencia de la prueba para diagnosticar o descartar la enfermedad dependerá del punto de corte elegido. Si calculáis los cocientes de probabilidades para el punto de corte p = 0.12, el positivo (CPP) es de 6.25 y el negativo (CPN) de 0.55, lo que sugiere un rendimiento modesto para el diagnóstico positivo y una aportación nula para el negativo.
Para conseguir un CPP > 10, tendríamos que elegir el corte en p = 0.25, pero la S disminuiría hasta un 0.25. No podríamos permitirnos tantos falsos negativos.
En cuanto al CPN, no podemos conseguir un valor bajo con ningún punto de corte.
Esta prueba lo tiene difícil para descartar la enfermedad. La causa está en el desequilibrio de las dos categorías a clasificar, en la baja prevalencia de la enfermedad. Tened en cuenta que, si decimos que todos los pacientes están sanos sin hacer ninguna prueba, acertaremos por azar el 95% de las veces.
Entonces, ¿tiene utilidad o no? Yo creo que sí. Pensad que estáis de guardia en un servicio de Urgencias y que queréis saber si los pacientes que acuden con determinado síntoma padecen esta grave enfermedad. No podéis hacerle la fildulastrina a todos, ya que es muy cara y molesta y, a fin de cuentas, la inmensa mayoría (el 95%) no va a padecer la enfermedad.
Pero tampoco es razonable hacer nada, ya que la enfermedad es muy grave y nos interesa diagnosticarla en sus fases iniciales, si es posible. Pues bien, esta prueba podría servirnos para identificar el grupo con un mayor riesgo de enfermedad, al que podríamos seguir en consulta, repetir la prueba pasado un tiempo o realizarle el patrón de referencia, según nos parezca más adecuado.
Nos vamos…
Y hasta aquí hemos llegado por hoy.
Creo que ha quedado claro que la elección del punto de corte para la positividad de una prueba diagnóstica depende, no solo de las características de la prueba, sino también del escenario clínico en el que se quiera aplicar.
Además, hemos comprobado cómo esta elección puede hacerse todavía más difícil cuando tratamos con prevalencias muy bajas, situaciones en los que los modelos estadísticos lo tienen más difícil para clasificar sanos y enfermos.
Finalmente, hemos visto una cómo la razón de enriquecimiento, una de las herramientas que vienen del campo de la ciencia de datos, puede ayudarnos en la elección del punto de corte en estas situaciones más complejas.
Esta no es la única herramienta a la que podemos recurrir para dirimir el delicado equilibrio entre la sensibilidad de una prueba y su precisión. Existen otras, con el F-score, con origen también en la ciencia de datos. Pero esa es otra historia…
Bibliografía
- Assessment of diagnostic tests. En: Palmas WR, ed. Pocket evidence based medicine. A survival guide for clinicians and students. Springer. NY, 2023; 15-33. (HTML)
- Linear and logistic regression. En: Zumel N, Mount J, eds. Practical Data Science with R, 2ª ed. Manning Publications Co. Shelter Island, NY, 2020;215-73. (HTML)