Cómo citar este artículo: Molina, M. (2024). El misterio de los calcetines desparejados: Calidad de un modelo de regresión lineal. Revista Electrónica AnestesiaR, 16(2). https://doi.org/10.30445/rear.v16i2.1240
Es increíble las vueltas que puede dar nuestra mente cuando la dejamos vagar a su antojo. Sin ir más lejos, el otro día yo me hacía una pregunta que me parece verdaderamente desconcertante: ¿por qué las personas insisten en llevar calcetines de diferentes colores?
Seguro que os ha pasado alguna vez. No importa cuán cuidadosamente seleccionemos nuestra ropa por la mañana, siempre parece haber un duende travieso que se burla de nuestra coordinación. Algunos podrían argumentar que es simplemente una expresión de creatividad audaz e inconsciente, mientras que otros creen que es una conspiración global para mantenernos a todos ligeramente desequilibrados.
Pero hoy no vamos a hablar de mis delirios mentales sobre el color de los calcetines. Y es que, en este mundo donde la moda y el caos se entrelazan en un baile inexplicable, nos encontramos con un desafío aún mayor: comprender y evaluar la calidad de un modelo de regresión lineal múltiple.
Así es.
Al igual que buscamos armonía en nuestros conjuntos de ropa, también anhelamos un modelo de regresión que se ajuste con precisión y nos brinde resultados confiables.
¿Cómo podemos distinguir entre un modelo mediocre y uno que destaque en términos de parámetros de calidad?
Seguidme en este viaje, donde exploraremos los secretos ocultos detrás de los coeficientes y descubriremos cómo medir la excelencia en el reino de la regresión lineal múltiple.
Modelo de regresión lineal múltiple
Ya vimos en entradas anteriores cómo los modelos de regresión intentan predecir el valor de una variable dependiente conociendo el valor de una o más variables independientes o predictoras. En el caso de una variable independiente, hablaremos de regresión simple, mientras que, si hay más de una, trataremos de regresión múltiple. Por último, recordemos que existen diferentes tipos de regresión en función del tipo de variable que queramos predecir.
Hoy vamos a centrarnos en la regresión lineal múltiple, cuya ecuación general es la siguiente:
Y = b0 + b1X1 + b2X2 + … + bnXn
En la que «Y» es el valor de la variable dependiente medida en una escala continua, «b0» es la constante del modelo (equivale al valor de la variable independiente cuando todas las dependientes valen cero o cuando no hay efecto de las variables independientes sobre la dependiente), «bi» los coeficientes de cada variable independiente (equivalen al cambio de valor de «Y» por cada unidad de cambio de «Xi») y «Xi» dichas variables independientes.
También vimos en una entrada anterior cómo el modelo de regresión lineal precisa que se cumplan una serie de requisitos para su correcta aplicación.
Estos son:
- el supuesto de linealidad (la relación entre variable dependiente e independientes debe ser lineal),
- el supuesto de homocedasticidad de los residuos del modelo (las diferencias entre los valores observados y los predichos por el modelo deben seguir una distribución normal con varianzas iguales a lo largo de todos los valores de las variables) el supuesto de normalidad de los residuos),
- y, por último, uno específico de la regresión múltiple, que no exista colinealidad (que no haya variables independientes correlacionadas entre sí).
Habitualmente, utilizamos programas estadísticos para la elaboración de los modelos de regresión, ya que es impensable hacerlos de manera manual. El problema está, en ocasiones, en valorar la gran cantidad de información sobre el modelo que el programa calcula y nos muestra.
Esto es así porque existen varios aspectos clave que debemos valorar para determinar su calidad y validez. Uno de ellos es la bondad de ajuste, que nos indica qué tan bien se ajustan los datos observados a las predicciones del modelo.
Además, debemos considerar la capacidad predictiva del modelo, evaluando su habilidad para generalizar y predecir nuevos valores con precisión.
Otro aspecto importante es la significación estadística de los coeficientes de regresión, que nos permite determinar si las variables independientes tienen un efecto informativo sobre la variable dependiente.
En resumen, al analizar un modelo de regresión lineal múltiple, debemos tener en cuenta la bondad de ajuste, la capacidad predictiva y la significación estadística de los coeficientes para obtener conclusiones sólidas y confiables, por lo que es esencial conocer los parámetros que nos informan sobre la calidad del modelo.
Un ejemplo práctico
Para desarrollar todo lo que hemos dicho hasta ahora, vamos a utilizar un ejemplo realizado con un programa estadístico concreto, el programa R. Vamos a elaborar un modelo de regresión lineal múltiple y analizar todos los resultados que el programa nos ofrece sobre el modelo.
Como es lógico, la salida de resultados variará en función del programa de estadística que empleemos, pero básicamente tendremos que analizar los mismos parámetros con independencia de cuál utilicemos.
Vamos a utilizar el conjunto de datos «iris» al que se recurre con frecuencia para la docencia con R, que contiene 150 registros con mediciones de longitud y anchura de pétalos (Petal.Length, Petal.Width) y sépalos (Sepal.Length, Sepal.Width) de tres especies (Species) de flores: setosa, versicolor y virgínica.
Supongamos que deseamos predecir la longitud del pétalo (Petal.Length) utilizando las variables independientes Sepal.Length, Sepal.Width, Petal.Width y Species.
Para ello, recurrimos a la función «lm()» para ajustar el modelo de regresión lineal múltiple.
La fórmula debe especificar que la longitud del pétalo (Petal.Length) es la variable dependiente, mientras que Sepal.Length, Sepal.Width, Petal.Width y Species son las variables independientes:
model <- lm(Petal.Length ~ Sepal.Length + Sepal.Width + Petal.Width + Species, data = iris)
El modelo se guarda en una variable llamada «model».
Para ver la información disponible, la forma más sencilla es ejecutar el comando summary(model). Podéis ver el resultado en la figura adjunta, que incluye información sobre los coeficientes, la significancia estadística y la bondad de ajuste del modelo.
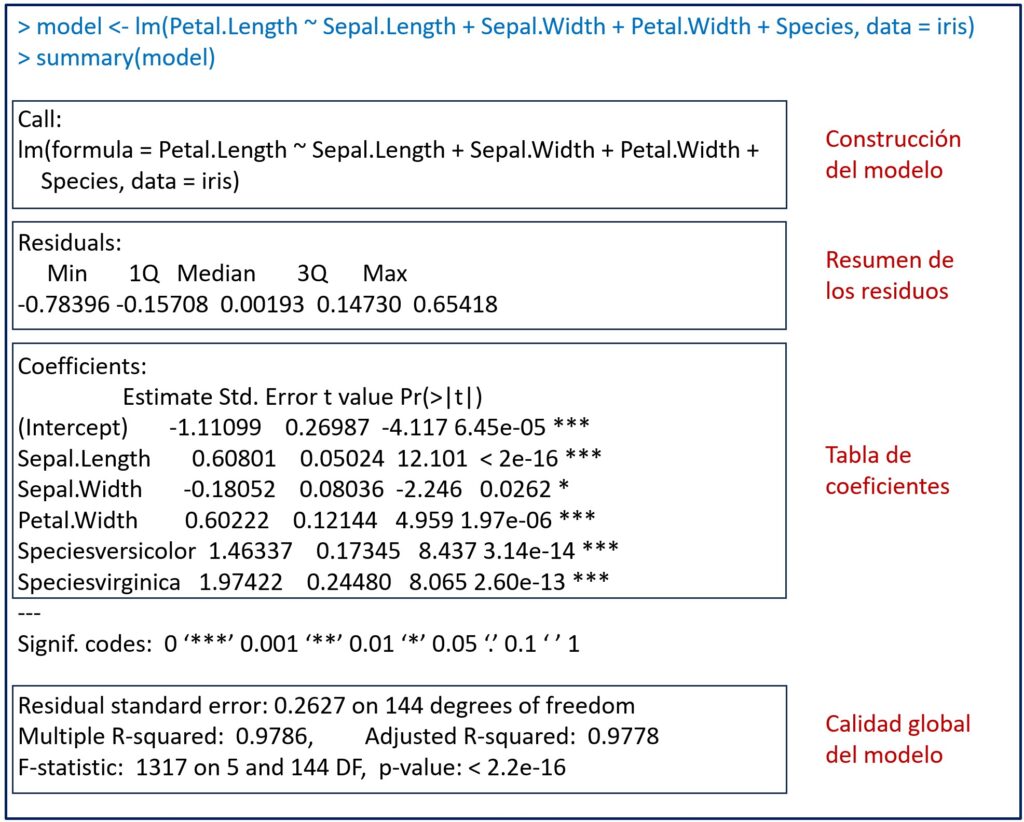
En la figura he añadido unos recuadros para separar los diferentes aspectos de la información del modelo que R nos proporciona. Vamos a verlos uno a uno.
Construcción del modelo
Lo primero que nos muestra la función summary() es la fórmula utilizada para construir el modelo. Este es el momento para revisar que la fórmula es la correcta, que hemos incluido en el modelo todas las variables independientes que deseamos y que hemos utilizado el conjunto de datos adecuado.
Según la sintaxis de R, la función lm() incluye la fórmula con la variable dependiente a la izquierda del símbolo «~» y la suma de las independientes a su derecha. Finalmente, especifica que hemos usado los datos del conjunto «iris».
Resumen de los residuos
A continuación, tenemos el resumen de los residuos del modelo de regresión. Ya sabemos que los residuos son los errores de predicción del modelo o, lo que es lo mismo, la diferencia entre los valores reales y los que predice el modelo, por lo que es fácil comprender que son un dato muy importante para valorar la calidad de ajuste del modelo.
El método más habitual para calcular los valores de los coeficientes de regresión del modelo es el llamado método de los mínimos cuadrados, que busca el valor mínimo de la suma de los cuadrados de los residuos.
De esta forma, lo que nos interesa es que el valor de los residuos sea lo más bajo posible (que haya mínimas diferencias entre los valores reales y los predichos por el modelo).
El programa nos proporciona los valores máximo y mínimo de los residuos, además de los tres cuartiles: el primer cuartil (el límite superior del 25% de los residuos ordenados de menor a mayor), la mediana o segundo cuartil (que deja a cada lado el 50% de los residuos), y el tercer cuartil (límite superior del 75% de los residuos).
La distribución de los residuos en los cuartiles nos da una idea de la distribución de los datos. Para que se cumpla el supuesto de normalidad de los residuos, la mediana tiene que ser próxima a cero y los cuartiles primero y tercero estar equidistantes de la mediana (y con un valor lo más bajo posible).
En nuestro caso, la mediana vale prácticamente cero y hay una distribución simétrica de los cuartiles primero y tercero, con valores no muy altos.
Fijaos el interés que tienen estos dos cuartiles, ya que definen el rango del 50% de los residuos del modelo. Si tomamos una predicción al azar, el residuo estará entre -0.157 y 0.147 el 50% de las veces. Esta será la magnitud frecuente del error del modelo, con lo que ya nos puede dar información sobre si es demasiado grande como para poder aplicarlo a nuestra práctica.
La tabla de coeficientes
Nos centramos ahora en la tabla de los coeficientes de regresión del modelo, con los coeficientes en las filas y una serie de columnas:
- 1. Nombre de la variable.
- 2. Valor estimado del coeficiente de regresión (estimate).
- 3. El error estándar del coeficiente (Std. Error), que nos permite calcular su intervalo de confianza).
- 4. La medida de significación estadística de cada coeficiente estimado, en forma del valor de «t»(t value). El valor t se calcula dividiendo el valor estimado del coeficiente entre su error estándar. Proporciona una indicación de cuántas desviaciones estándar se aleja el coeficiente estimado de cero (el supuesto de la hipótesis nula es que los coeficientes no son distintos de cero). En general, cuanto mayor sea el valor absoluto del valor «t», más significativo es el coeficiente.
- 5. El valor de «p» (Pr(>|t|)), que nos dice la probabilidad de encontrar un valor de «t» tan alejado o más de cero solo por azar. Como ya sabemos, lo habitual es considerar esta diferencia como estadísticamente significativa cuando p < 0.05.
Este valor puede verse falseado si existe colinealidad, que puede hacer incluso que se pierda la significación estadística del coeficiente de una variable que sí intervenga en la capacidad de ajuste del modelo.
Una pista que nos puede hacer sospechar que haya colinealidad es la presencia de coeficientes anormalmente grandes en comparación con los demás, de signo opuesto al que nos parecería que debería tener por nuestro conocimiento del contexto en el que se aplica el modelo, o con un error estándar muy alto.
Lógicamente, todo esto da por sobreentendido que hemos comprobado antes que se cumple el supuesto de normalidad de los residuos, como ya comentamos.
En estos casos, el modelo global puede incluso hacer predicciones correctas, pero nuestra interpretación sobre cuáles son las variables que más contribuyen a su capacidad explicativa puede verse falseada por la presencia de variables independientes correlacionadas.
Echemos un vistazo a nuestros coeficientes.
Tenemos el intercepto y cinco variables independientes, las tres cuantitativas (Sepal.Length, Sepal.Width y Petal.Width) y dos coeficientes para la variable Species.
La variable Species es una cualitativa con tres categorías: setosa, versicolor y virgínica.
Lo que ha hecho el programa es tomar la setosa como referencia (la primera categoría en orden alfabético) y crear dos variables indicadoras o dummies: Speciesversicolor (vale 1 si la especie es versicolor) y Speciesvirginica (vale 1 si la especie es virginica).
Vemos que todos los coeficientes, incluido el intercepto, tienen valores de p < 0.05, por lo que todos son estadísticamente significativos. No caigáis en la tentación de considerar mejores coeficientes aquellos con los valores de «p» más bajos. Una vez que el valor de «p» está por debajo del umbral que por consenso consideramos significativo, nos da igual lo pequeño que sea.
Así, nuestra ecuación de regresión quedaría de la siguiente manera:
Petal.Length = -1.11 + 0.60 x Sepal.Length – 0.18 x Sepal.Width + 0.60 x Petal.Width + 1.46 x Speciesversicolor + 1.97 x Speciesvirginica
El significado de las variables cuantitativas es más sencillo de interpretar.
Por ejemplo, 0.60 x Sepal.Length quiere decir que, manteniendo el resto de las variables constantes, cada unidad de aumento de la longitud del sépalo contribuye a 0.6 unidades de aumento de la longitud del pétalo (la variable dependiente).
Para un mismo valor de las variables cuantitativas independientes, una flor versicolor tendrá una longitud del pétalo 1.46 unidades mayor. Por su parte, si la flor es una virginica, este aumento de la longitud del pétalo será de 1.97 unidades.
Resumen de la calidad global del modelo
La última parte de la salida de resultados de la función summary() nos muestra las estadísticas de calidad del modelo global. Es muy importante comprobar la calidad de los indicadores de este apartado antes de aplicar el modelo y no basarse únicamente en la significación estadística de los coeficientes de regresión.
Los parámetros que debemos valorar son los siguientes:
1. Los grados de libertad (degrees of freedom).
El número de grados de libertad del modelo se calcula restando al número de observaciones el número de coeficientes del modelo. En nuestro ejemplo tenemos 150 observaciones y 6 coeficientes, luego el modelo tiene 144 grados de libertad.
Si os fijáis, los grados de libertad nos informan de la relación entre el número de observaciones y el número de variables independientes que introducimos en el modelo. Como es lógico, nos interesará que el número de grados de libertad sea lo más alto posible, ya que un numero bajo indicaría que el modelo puede ser demasiado complejo para la cantidad de datos de que disponemos, con lo que el riesgo de sobreajuste del modelo (ovefitting) será muy alto.
2. Error estándar de los residuos (Residual standard error).
Es la suma de los cuadrados de los residuos dividido entre el número de grados de libertad. Es similar a la suma de cuadrados de los residuos utilizado por el método de los mínimos cuadrados, pero ajustado por el tamaño de la muestra al dividirlo entre los grados de libertad.
El utilizar el error estándar de los residuos —y no su suma de cuadrados— es un intento más de ajustar el parámetro según la complejidad del modelo. Los valores más altos indicarán modelos más complejos (menos grados de libertad y, por tanto, mayor número de variables independientes respecto al número de observaciones) que tendrán mayor riesgo de sobreajuste y peor capacidad de generalización de predicciones.
3. R2 múltiple y ajustado.
El R2, o coeficiente de determinación, es otra medida importante de la bondad de ajuste del modelo. Este parámetro explica la varianza total del conjunto de datos que el modelo es capaz de explicar.
Veamos una forma sencilla de calcularlo para entender mejor su significado.
Volviendo a los datos de nuestro ejemplo, cualquier modelo de predicción que desarrollemos tendrá que funcionar mejor que lo que los estadísticos llaman «el modelo nulo». En este caso, el modelo nulo estaría representado por la media de la longitud de los pétalos de todas las flores de nuestra muestra. Así, una estimación sencilla sería predecir que una flor elegida al azar tiene una longitud de pétalo igual a este valor medio.
Esta estimación es muy sencilla, pero también será muy inexacta (tanto más cuanta mayor variabilidad haya en el tamaño de las flores). De todas maneras, aunque el modelo nulo no sea muy bueno, lo tomamos como referencia a batir con los modelos que podamos desarrollar.
Si calculamos la suma de los cuadrados de los residuos del modelo nulo obtendremos la llamada suma total de cuadrados (SST, de sus siglas en inglés), que es la varianza total de los datos que estamos estudiando.
Nosotros lo que pretendemos es desarrollar un modelo cuya suma de cuadrados de residuos (SSR) sea mucho menor que la varianza total (SST). Esto es lo mismo que decir que queremos que el cociente entre SSR y SST sea lo menor posible (lo más próximo posible a 0). Para poder interpretarlo con más facilidad, calculamos el coeficiente de determinación como el complementario de este cociente, según la sencilla ecuación que os muestro a continuación:
R2 = 1 – (SSR / SST)
Por tanto, el R2 compara la varianza de nuestro modelo con la varianza total de los datos, por lo que nos informa del porcentaje de variabilidad de los datos que explica el modelo. Su valor puede oscilar desde 0 (el peor modelo) hasta 1 (un modelo con un ajuste perfecto).
Pero el coeficiente de determinación tiene un pequeño inconveniente: si aumentamos mucho el número de variables independientes del modelo, el valor del coeficiente se ve magnificado aún a pesar de que las variables no sean muy informativas.
Si lo pensáis, esto es lo mismo que ya hemos dicho varias veces. Los modelos más complejos tienen tendencia a parecer mejores porque suelen realizar un sobreajuste de los datos, pero generalizarán peor las predicciones cuando apliquemos posteriormente el modelo a nuestro entorno.
Por esta razón se calcula el llamado coeficiente de determinación ajustado, que es un estimador más conservador que el R2 de la bondad de ajuste del modelo. Además, puede servirnos para comparar la bondad de ajuste cuando se comparan modelos de diferente número de variables independientes o predictoras realizados a partir de los mismos datos.
La fórmula, para aquellos adictos a las matemáticas, es la siguiente:
R² ajustado = 1 – [(1 – R²) x (n – 1) / (n – p – 1)],
donde «n» es el número de observaciones y «p» el número de variables independientes.
Si nos fijamos en nuestro ejemplo, los valores de los dos coeficientes son muy similares, pero eso es porque estamos utilizando un modelo bastante sencillo. Con datos más numerosos y un número alto de variables independientes, esta diferencia suele hacerse más llamativa.
4. La significación del modelo.
La información de la función summary() termina con el contraste sobre la significación estadística del modelo global.
De igual manera que se usaban los valores de «t» para calcular la significación estadística de los coeficientes de regresión del modelo, se utiliza una F de Snedecor para contrastar la significación del modelo global.
Como ya sabemos, la F compara el cociente de dos varianzas. En este caso, la varianza de los residuos del modelo nulo frente a la varianza de los residuos de nuestro modelo, que queramos que sean lo más diferentes posibles. Mediante el valor de «p», el programa estima la probabilidad de que observemos un estadístico F tan grande o mayor que el observado bajo el supuesto de la hipótesis nula de que numerador y denominador son iguales (F = 1).
No hace falta repetir que nos interesa que sea menor que el valor elegido como umbral para la significación estadística que, por convenio, suele ser p < 0.05. En este caso, el modelo es estadísticamente significativo.
Para ir terminando, hacer solo mención de que el hecho de que el modelo sea estadísticamente significativo no quiere decir que se ajuste bien a los datos, sino que, simplemente, es capaz de predecir mejor que el modelo nulo.
En ocasiones, un modelo con una F significativa y un valor de R2 bajo nos indicará que, aunque el modelo funciona, su capacidad de hacer predicciones (su bondad de ajuste) no es buena. Seguramente haya, en casos similares, más variables implicadas en el comportamiento de los datos y que no hemos incluido en el modelo (aunque también puede ocurrir que el tipo de modelo elegido no es el más adecuado para explicar nuestros datos).
Nos vamos…
Y aquí lo vamos a dejar por hoy.
Hemos visto cómo leer e interpretar de forma correcta toda la información sobre la bondad de ajuste y la calidad de los modelos de regresión lineal múltiple que nos proporcionan los programas informáticos.
Lógicamente, y como ya hemos comentado, todo esto debe completarse con un correcto diagnóstico del modelo para comprobar que se cumplen los supuestos necesarios para su aplicación.
Hemos hablado también de cómo la existencia de multicolinealidad entre las variables independientes puede sesgar el valor de los coeficientes y dificultar la interpretación del modelo.
En estos casos, lo ideal será no introducir variables correlacionadas y simplificar el modelo. Pero esto no siempre es fácil o conveniente. Para estas situaciones podremos contar con las llamadas técnicas de regularización de la regresión lineal, como la regresión de lasso o la regresión de ridge.
Pero esa es otra historia…



1 Comment