Anoche soñé que volvía a Manderley. Me encontraba ante la verja del parque, pero durante algunos momentos no pude entrar…
Bueno, en realidad, eso no me pasó a mí, sino a Rebeca, como los aficionados al cine o la literatura ya habrán reconocido.
Yo, en realidad, volví a tener uno de mis sueños lovecraftianos en los que me encontraba perdido dentro de un laberinto en el país de los números. Allí estaba yo, sumergido en un mar de dimensiones desconocidas, donde las variables predictoras se entrelazaban en un baile caótico de incertidumbre. No había manera de salir del laberinto: cada esquina me llevaba a una nueva dimensión de posibilidades, y ninguna salida parecía a la vista.
Si en mi sueño me hubiese acordado de Rebeca, podría haberme sentido dotado de una fuerza sobrenatural y atravesar como un espíritu las paredes del laberinto. Pero claro, una mente cuadriculada y nada poética como la de un servidor, solo pudo recurrir a una herramienta mucho más pragmática, aunque no por ello menos original dentro de mi universo onírico.
Así que empecé a elaborar un árbol de decisión que pudiera convertir las bifurcaciones del laberinto en opciones claras y definidas y cuyas ramas se extendiesen, como hilos de Ariadna, guiándome a través del enigma de las variables hacia una claridad que antes parecía inalcanzable.
El árbol fue mi brújula de salvación en el universo multidimensional en el que me encontraba, llevándome paso a paso hacia la salida del laberinto de las variables predictoras. Así escapé del laberinto de mis sueños. Al despertar comprendí que, si utilizas la herramienta adecuada, incluso en los mundos más extraños y desconocidos, siempre hay una forma de encontrar el camino hacia la claridad y la certeza.
Y como imagino que, después de este desvarío, estaréis deseando conocer qué son y cómo funcionan los árboles de decisión, os invito a que sigáis leyendo esta entrada.
Los árboles de decisión
Un árbol de decisión es un modelo de aprendizaje automático que se utiliza para clasificar o predecir una variable objetivo basándose en varias variables de entrada.
Los árboles trabajan estratificando el espacio de las variables predictoras en una serie de zonas o regiones. Manteniendo el símil de la jardinería, la sistemática de trabajo se parecería más a la forma de dividir el jardín de los datos en parcelas para que, al tener un dato nuevo, la predicción para ese valor con ese conjunto de variables predictoras sea el valor medio de la variable objetivo de esa parcela.
Esto se muestra de manera gráfica en forma de un árbol, donde cada nodo interno representa una característica que nos permite separar cada parcela y cada rama representa una decisión basada en esa característica. Finalmente, cada hoja o nodo terminal representa el resultado de la decisión o la clasificación final. Y, no os lo he dicho, el árbol se dibuja cabeza abajo, con la raíz arriba y las hojas en la parte inferior.
Para entenderlo mejor, vamos a poner un ejemplo usando el conjunto de datos “mtcars”, al que se recurre con frecuencia para la docencia con R, que contiene información sobre diferentes modelos de automóviles y sus características. Incluye 32 filas (una por cada modelo) y 11 columnas que representan diversas características de los automóviles, como la eficiencia del combustible (mpg), el número de cilindros (cyl), la cilindrada (disp), la potencia del motor (hp), la relación de ejes traseros (drat), el peso (wt), etc.
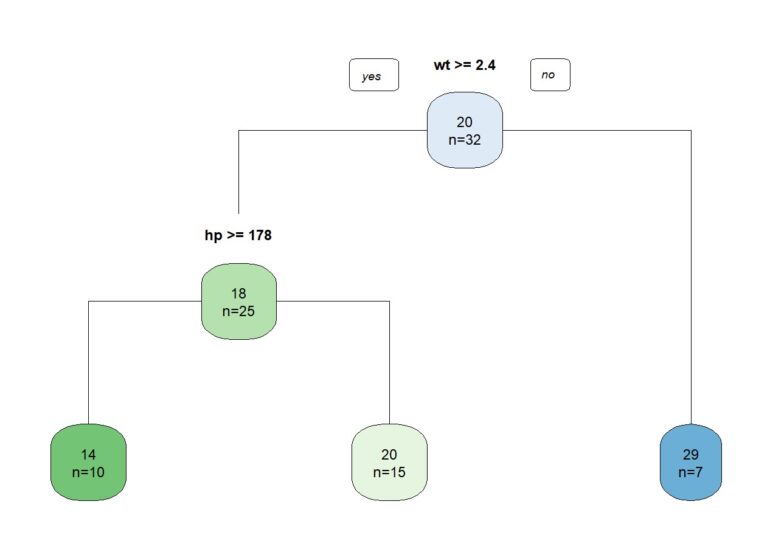
Supongamos que deseamos predecir la eficiencia del combustible (millas por galón, mpg) utilizando las variables independientes peso (wt) y potencia del motor (hp). En la figura 1 podéis ver el sencillo árbol de decisión que elaboramos con el programa R.
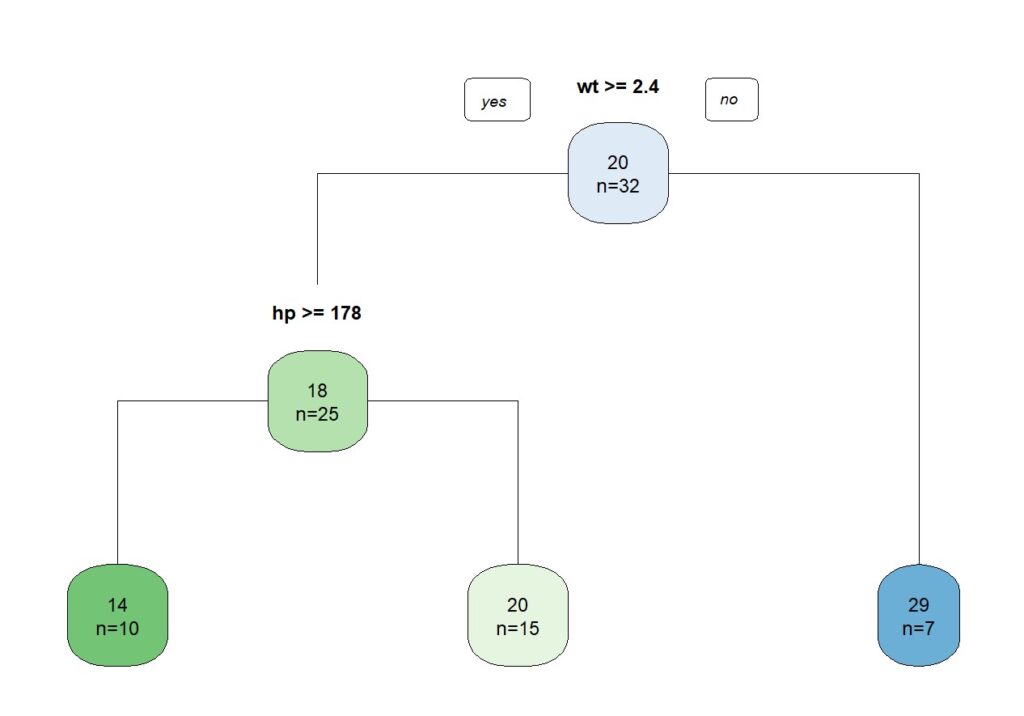
Lo primero que miramos es si el peso del coche es igual o superior a 2400 libras. Si el coche pesa menos de esa cantidad, será capaz de recorrer, por término medio, 29 millas con un galón de combustible. La potencia del motor importa menos es este grupo de automóviles más ligeros.
Pero si el coche pesa más de 2400 libras, sí que importa su potencia. Aquellos con menos de 178 caballos recorrerán, de media, 20 millas por cada galón, mientras que los que tengan una potencia superior a los 178 caballos consumirán más combustible y tendrán menos eficiencia: solo 14 millas por cada galón de combustible, de media.
Vemos una de las grandes ventajas de los árboles de decisión, que es su fácil interpretación (sobre todo si hay pocas variables y el árbol no es muy frondoso). Pero, en realidad, lo que hace el modelo es dividir en parcelas el espacio de variables predictoras, tal como podéis ver en la segunda figura.
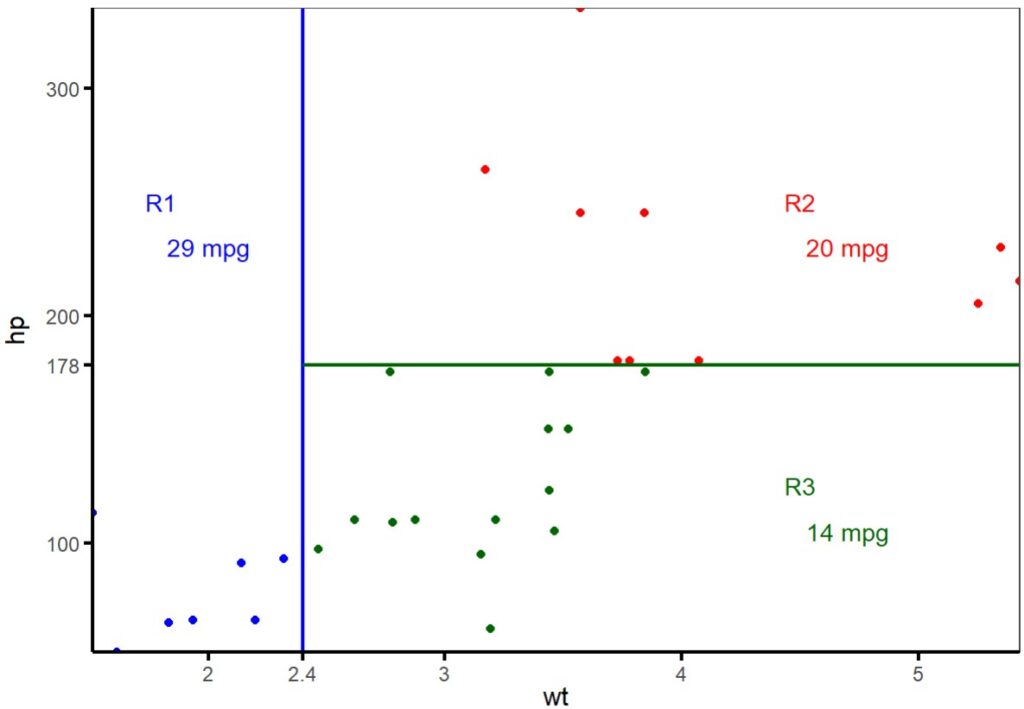
Inicialmente delimita una primera región (R1) para el peso de menos de 2400 libras. La eficiencia media de los coches de esta región es de 29 mpg. El espacio restante es, a su vez, dividido en otras dos regiones (R2 y R3) según el límite de los 178 caballos, marcando los dos grupos con un consumo de medio de 20 y 14 mpg, respectivamente.
Una vez que tengamos un nuevo coche del que queramos estimar su eficiencia energética, solo tendremos que aplicar este sistema y asignarle a la zona a la que pertenezca. Así, la predicción de su eficiencia energética será la del valor medio de la zona a la que corresponde.
Como es lógico, cuantas más variables se incluyan en el modelo, más podremos afinar las predicciones. Este ejemplo es muy sencillo para poder mostrar gráficamente cómo dividimos un espacio bidimensional y entender mejor el concepto, pero, en la realidad, manejaremos espacios multidimensionales de variables predictoras para estimar el valor de la variable objetivo de los datos nuevos que queramos estimar.
Lo siguiente que nos vamos a plantear es cómo se calculan las regiones para construir el árbol de decisión. Veámoslo.
Construyendo árboles
Ya hemos visto que el objetivo es dividir el espacio de variables predictoras en una serie de cajas multidimensionales o regiones, de forma que a los nuevos elementos se les asigna el valor medio de la región a la que pertenecen. ¿Cómo sabemos que regiones son las mejores?
Para calcular estas regiones se utiliza un sistema muy querido en el mundo de los algoritmos y modelos de estadística y ciencia de datos: una variación del método de los mínimos cuadrados.
El árbol se elabora con un conjunto de datos del que se conocen tanto las variables predictoras como la variable objetivo que queremos estimar. Una vez construido el modelo, comparamos los valores que el árbol predice con los valores reales.
La diferencia de estos valores (los residuos) se elevan al cuadrado y se suman, de forma muy parecida a como se hace, por ejemplo, para estimar los coeficientes de un modelo de regresión lineal. Primero se obtiene una suma para cada región y, después, se suman las de todas las regiones para obtener la suma de cuadrados.
El objetivo será encontrar el árbol con el que se obtenga el valor más bajo de esta suma de cuadrados. El problema es que sería computacionalmente muy costoso calcular las sumas de cuadrados de todos los árboles posibles (con todas las combinaciones de las variables predictoras en las diferentes regiones).
Para solucionar este problema, se realiza lo que se llama un enfoque ávido (greedy aproach para los amantes de Albión) que, empezando de arriba a abajo, toma decisiones locales óptimas en cada paso sin considerar las consecuencias globales, con el objetivo de encontrar una solución generalmente aceptable en ese punto.
Así, comienza considerando todos los predictores y todos sus puntos de corte posibles, calculando las sumas de cuadrados de los residuos y seleccionando aquel con el valor mínimo. Aquí se realiza la primera partición del espacio de las variables predictoras.
A continuación, esto se repite sucesivamente, generando el resto de las regiones, equivalentes a las ramas que salen de cada nodo del árbol. El enfoque se llama “ávido” porque elige cada partición en un momento en que resulta favorable, pero sin considerar si resultaría mejor utilizar este criterio más abajo en el árbol.
Recortando el árbol
Aunque el procedimiento recursivo que acabamos de ver puede proporcionar buenas predicciones, en ocasiones puede dar lugar a sobreajuste de los datos y a un árbol más complejo y difícil de interpretar, como el que veis en la figura 3.
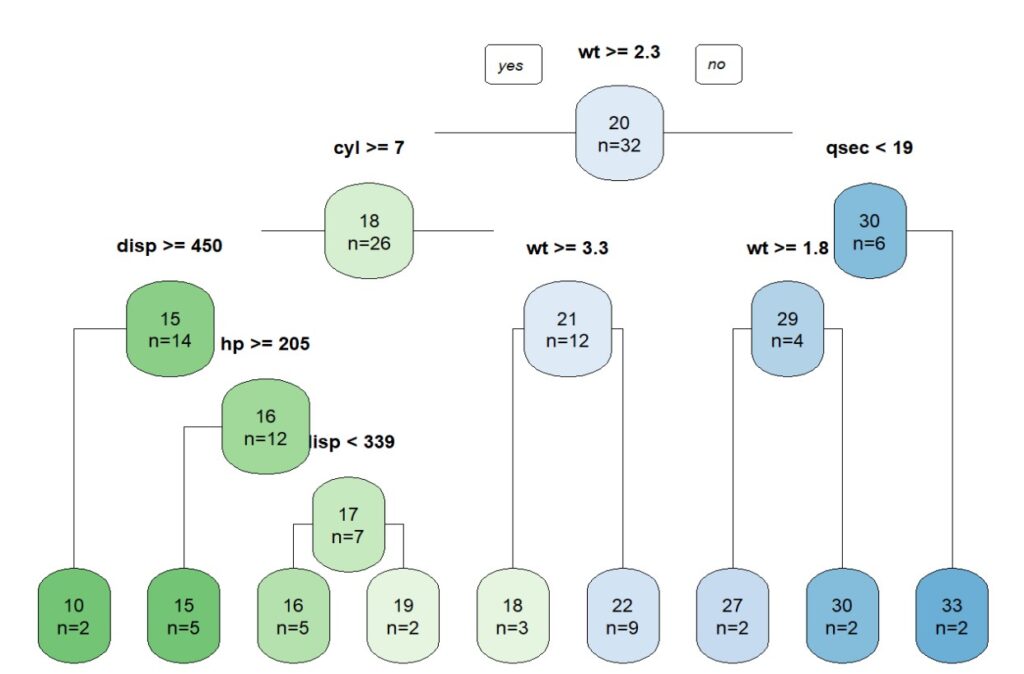
En estos casos, tenemos varias alternativas. La primera es construir, de entrada, un árbol más sencillo. Por ejemplo, podemos empezar a dividir el espacio de variables predictoras hasta que alcancemos un número predeterminado de nodos, de casos por hoja final o un valor determinado de la suma de cuadrados de los residuos del que no necesitemos bajar.
Otra posibilidad es construir un árbol completo muy complejo y proceder a recortar algunas de sus ramas, considerando todos los sub-árboles y sus sumas de cuadrados. El problema, podría ser muy costoso desde el punto de vista computacional.
Una opción más práctica es recurrir a un truco similar al utilizado para estimar los coeficientes de la regresión lasso: penalizar la función de mínimos cuadrados sumándole un factor que sería el producto del número de nodos terminales deseados por un parámetro llamado alfa, que actuaría como la balanza entre la complejidad del árbol y su capacidad predictiva.
Cuando α = 0, el árbol que obtenemos es el completo. Sin embargo, cuando α aumenta, se penaliza la función de mínimos cuadrados y se genera un árbol con menos ramas. Podemos generar varios árboles con valores sucesivos de α y elegir aquel que mejor pondere, según nuestro criterio, los aspectos de complejidad y precisión que nos interesen.
Árboles de decisión para clasificación
Todo lo que hemos visto hasta ahora se refería a árboles de decisión diseñados para estimar o predecir el valor de una variable cuantitativa. En otras palabras, hemos hablado de los árboles de decisión para regresión. Pero los árboles pueden servir también como métodos de clasificación, que es lo mismo que decir que pueden estimar una variable de respuesta cualitativa.
En estos casos, el método de elaboración sigue un razonamiento similar al de los árboles de regresión, pero tiene algunas diferencias, sobre todo en la función de error que usamos para construir el árbol.
Para mostraros un ejemplo de clasificación, voy a utilizar el conjunto de datos “Pima.te”, del paquete MASS de R.
Este conjunto de datos contiene un registro de 332 mujeres gestantes mayores de 21 años que son evaluadas para un diagnóstico de diabetes gestacional según los criterios de la OMS. Además del diagnóstico de diabetes (sí/no), contiene información sobre el número de gestaciones, glucemia plasmática, presión arterial sistólica, pliegue tricipital, índice de masa corporal, antecedente de diabetes y edad.
En este conjunto de datos hay 109 diabéticas y 223 no diabéticas. Podéis ver el árbol de decisión en la figura 4.
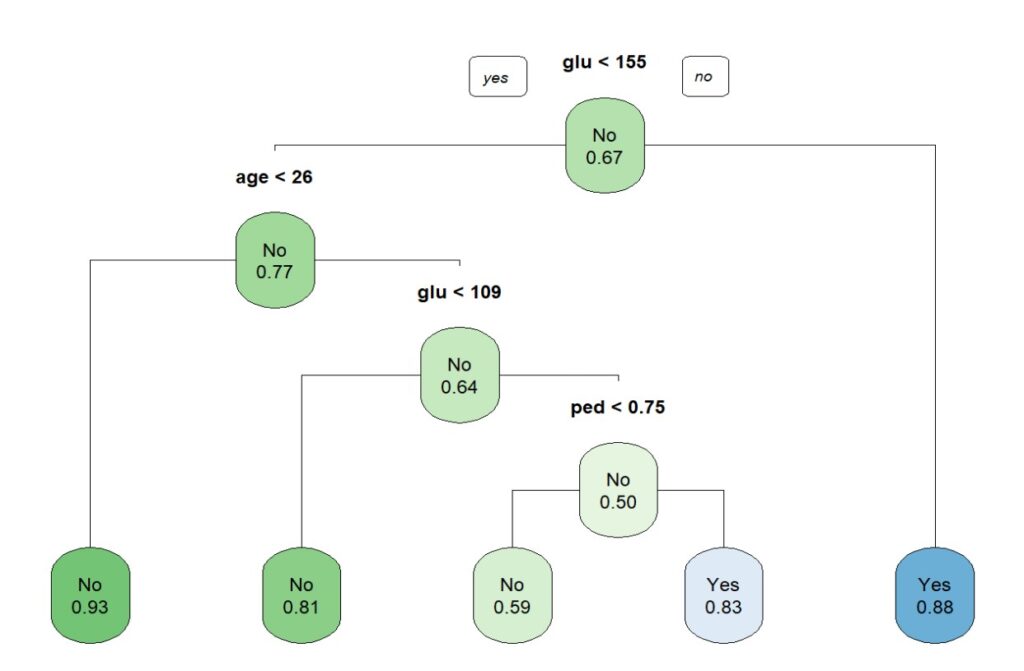
Al tratarse de un algoritmo de clasificación, en los nodos terminales no vemos el valor estimado, como en el caso anterior, sino la probabilidad de pertenecer a la categoría especificada. Por ejemplo, una mujer con glucemia de menos de 155 y edad menor de 26 años, tiene una probabilidad de NO ser diabética del 93% (o un 7% de ser diabética).
Construyendo árboles para clasificación
El mecanismo es similar a los pasos recursivos que hemos visto para los árboles de regresión, pero no nos sirve el criterio de minimizar la suma de los cuadrados de los residuos que empleamos antes.
Una posibilidad sería calcular el porcentaje de errores de clasificación, que sería la proporción de valores de una región que no pertenecen a la categoría mayoritaria de esa región. Este método es relativamente sencillo, pero, en la práctica, no es lo suficientemente sensible para producir árboles con buena capacidad de predicción.
En su lugar, se utilizan dos índices que se han desarrollado para este fin: el índice de Gini y el índice de entropía. Veamos en qué consisten.
Índice de Gini
El índice de Gini mide la varianza total que existe entre las diferentes categorías de la variable cualitativa de respuesta. Por este motivo, su valor tiende a cero cuando aumenta la proporción de casos de un nodo terminal que pertenecen a una categoría determinada. Es por lo que se considera al índice de Gini como una medida de la pureza del nodo.
Por ejemplo, si nos fijamos en los dos primeros nodos de la figura 4, el primero (con un 67% de no diabéticas) se considera de menor pureza que el segundo (77% de no diabéticas). Cuanto más bajo sea el índice de Gini, el nodo contendrá una mayor proporción de observaciones de la misma clase.
Índice de entropía
En este índice, inspirado en la teoría de la información, la entropía se refiere a la medida de incertidumbre o desorden en un conjunto de datos. En este contexto, se trata de determinar cómo se dividen los datos entre los diferentes nodos del árbol, con el objetivo de maximizar la homogeneidad de las clases dentro de cada nodo, que es lo mismo que minimizar la entropía.
Si lo pensamos un poco, es prácticamente lo mismo que trata de hacer el índice de Gini, por lo que no es de extrañar que, en la práctica, ambos tengan un valor numérico similar.
Las tres formas de cuantificar el error pueden utilizarse para elaborar los árboles, aunque hay autores que prefieren el índice de Gini o el de entropía para la elaboración y recurrir al porcentaje de errores de clasificación cuando se trata de recortar un árbol ya construido.
Nos vamos…
Y con esto vamos a ir dejando la jardinería por el día de hoy.
Hemos visto la sistemática que emplea el algoritmo de los árboles de decisión para ir dividiendo recursivamente el espacio de las variables predictoras para poder estimar o predecir el valor de la variable de respuesta objetivo, que puede ser tanto numérica (árboles de regresión) como nominal (árboles de clasificación).
Como muchos ya habréis pensado, este tipo de predicciones son las mismas que podemos hacer con modelos de regresión lineal o logística (en realidad, la regresión logística no es un método de regresión, sino de clasificación). ¿Qué tal funcionan los árboles respecto a los métodos más clásicos con los que estamos más familiarizados?
Pues, como siempre, dependerá del problema que estemos analizando. Si queremos predecir una variable numérica y nuestros datos se ajustan bien a un modelo lineal, la regresión funcionará mejor que los árboles. Sin embargo, si los datos siguen una relación no lineal más compleja, es posible que mejoremos nuestras predicciones usando árboles de decisión.
Aunque los árboles tienen la indudable ventaja de su interpretación y visualización gráfica, no suelen alcanzar valores de precisión tan altos como otros modelos de regresión o clasificación. Además, no son muy robustos en el sentido de que pequeños cambios en los datos pueden tener como consecuencia grandes variaciones en los árboles que construyamos.
Claro que todo esto puede mejorarse de manera sustanciosa empleando aquel viejo principio que dice que la unión hace la fuerza. Me estoy refiriendo al uso de árboles que emplean técnicas de remuestreo agregativo (bagging), bosques aleatorios (random forest) y otros métodos de ensamblaje de árboles de decisión. Pero esa es otra historia…
BIBLIOGRAFÍA
– Tree-based methods. En: James G, Witten D, Hastie T, Tibshirani R, eds. An introduction to statistical learning with applications in R. Springer Science+Business Media. New York, 2013; 303-35. (HTML)
– Supervised learning. En: Mailund T, ed. Beginning data science in R 4. Data analysis, visualization, and modelling for the data scientist, 2ª ed. Apress Media, LLC. New York, 2022; 178-238. (HTML)