Otra piedra con la que no tropezar. El método de Bland-Altman para medir acuerdo

Manuel Molina Arias
Servicio de Gastroenterología
Hospital Infantil Universitario La Paz. Madrid

Dice el refrán que el hombre es el único animal que tropieza dos veces con la misma piedra. Dejando aparte las connotaciones del uso de la palabra animal, la frase quiere dar a entender que podemos cometer muchas veces el mismo error, aún a pesar de darnos cuenta de ello. Dándose cuenta o no, en estadística hay una serie de errores que se cometen con mucha frecuencia, utilizando parámetros o pruebas estadísticas de forma incorrecta, ya sea por ignorancia o, lo que es peor, para obtener resultados más llamativos.

Un caso frecuente es el uso del coeficiente de correlación de Pearson para estudiar el grado de acuerdo entre dos formas de medir una variable cuantitativa. Veamos un ejemplo.

Supongamos que queremos valorar la fiabilidad de un nuevo tensiómetro de muñeca para medir la presión arterial. Tomamos una muestra de 300 escolares sanos y les medimos la presión dos veces. La primera con un manguito convencional de brazo, obteniendo una media de presión sistólica de 120 mmHg. y una desviación estándar de 15 mmHg. La segunda, con un nuevo tensiómetro de muñeca, con el que obtenemos una media de 119,5 mmHg. y una desviación estándar de 23,6 mmHg. La pregunta que nos hacemos es la siguiente: considerando el manguito de brazo como patrón de referencia, ¿es fiable la determinación de presión arterial con el de muñeca?

Podría pensarse que para contestar a esta pregunta se podría calcular el coeficiente de correlación entre ambos, pero cometeríamos un error de los gordos. El coeficiente de correlación mide la relación entre dos variables (cómo varía una cuando varía la otra), pero no su grado de acuerdo. Pensad, por ejemplo, si cambiamos la escala de uno de los dos métodos: la correlación no se modifica, pero el acuerdo que hubiese puede perderse por completo.

¿Cómo podemos saber entonces si la técnica nueva es fiable comparada con la convencional? Lo lógico es pensar que los dos métodos no van a coincidir siempre, así que lo primero que debemos preguntarnos es cuánto es razonable que difieran para dar validez a los resultados. Esta diferencia debe definirse antes de comparar los dos métodos y de establecer el tamaño muestral necesario para hacer la comparación. En nuestro caso vamos a considerar que la diferencia no debe ser mayor a una desviación estándar de lo obtenido con el método de referencia, que es de 15 mmHg.

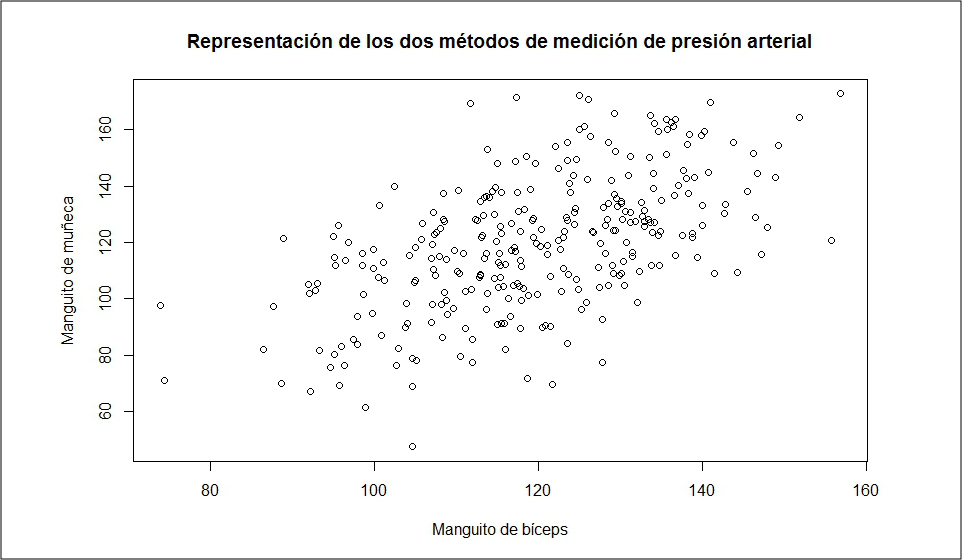
El primer paso que podemos dar es examinar los datos. Para ello hacemos un diagrama de puntos representando los resultados obtenidos con los dos métodos (Figura 1). Parece que hay cierta relación entre las dos variables, de forma que aumentan y disminuyen las dos en el mismo sentido. Pero esta vez no caemos en la trampa de dibujar la línea de regresión, que solo nos informaría de la correlación entre las dos variables.

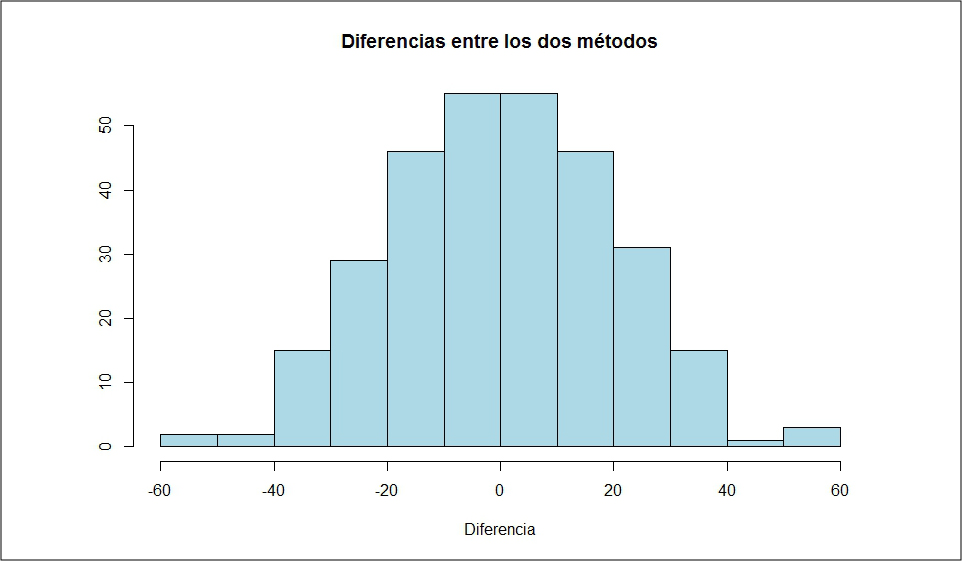
Otra posibilidad es examinar cómo son las diferencias. Si existiese un buen acuerdo, las diferencias entre los dos métodos se distribuirían de forma normal alrededor del cero. Podemos comprobar esto haciendo el histograma con las diferencias de las dos medidas, como veis en la figura 2. En efecto, parece que su distribución se ajusta bastante bien a una normal.

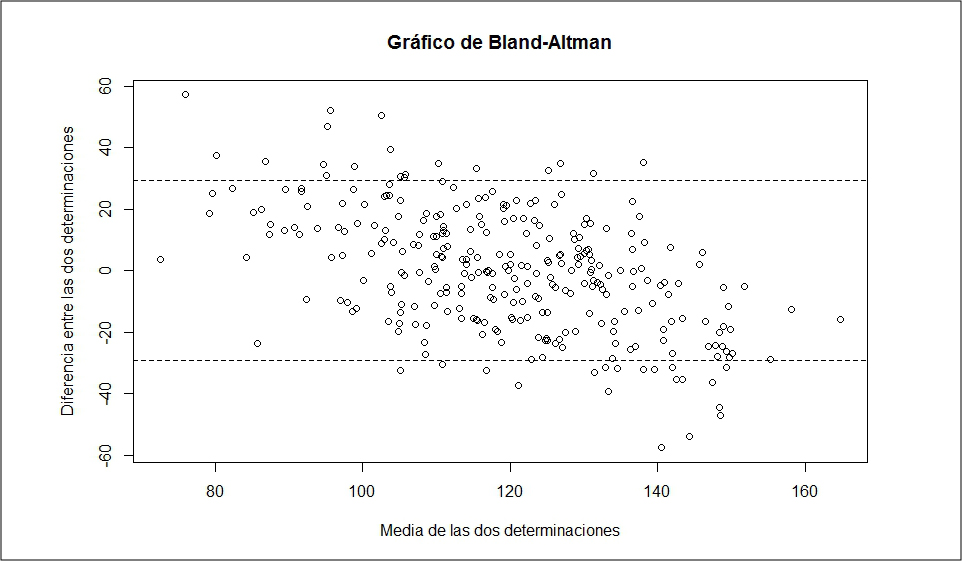
De todas formas, seguimos sin saber si el acuerdo es lo suficientemente bueno. ¿Qué tipo de gráfico nos puede servir? Lo que nos dará más información será representar la media de cada pareja de mediciones frente a su diferencia, construyendo así el llamado gráfico de Bland-Altman que podéis ver en la figura 3.

Como puede verse, los puntos se agrupan, más o menos, alrededor de una línea (en el cero) con un grado de dispersión que vendrá determinado por la amplitud de las diferencias de resultados entre los dos métodos. Cuanta mayor sea ese grado de dispersión, peor será el acuerdo entre los dos métodos. En nuestro caso, hemos dibujado las líneas que coinciden con una desviación estándar por debajo y por encima de la media cero, que eran los límites que considerábamos como aceptables entre los dos métodos para considerar un buen acuerdo.

Como veis hay bastantes puntos que caen fuera de los límites, así que tendríamos que valorar si el nuevo método reproduce los resultados de forma fiable. Otra posibilidad sería dibujar las líneas horizontales que engloban la gran mayoría de los puntos y considerar si estos intervalos tienen utilidad desde el punto de vista clínico.

El método de Bland-Altaman permite, además, calcular los intervalos de confianza de las diferencias y estimar la precisión del resultado. Además, hay que fijarse que el grado de dispersión sea uniforme. Puede ocurrir que el acuerdo sea aceptable en determinado intervalo de valores pero no lo sea en otro (por ejemplo, valores muy altos o muy bajos), en los que la dispersión sea inaceptable. Este efecto puede corregirse a veces transformando los datos (por ejemplo, transformación logarítmica), aunque siempre habrá que valorar considerar la utilidad de la medición en ese intervalo. Si miramos en nuestro ejemplo, parece que el tensiómetro de muñeca da valores más altos para sistólicas más bajas, mientras que da valores más bajos cuando la presión sistólica es mayor (la nube de puntos tiene una discreta pendiente negativa de izquierda a derecha). El método sería más fiable para sistólicas en torno a 120 mmHg, pero perdería reproducibilidad según se aleje el valor de presión arterial sistólica de los 120 mmHg.

Otra utilidad del método de Bland-Altman es la de representar las parejas de resultados de las mediciones hechas con el mismo método o instrumento, para así comprobar la reproducibilidad de los resultados de la prueba.

Y con esto termino lo que quería contaros del método de Bland-Altman. Antes de acabar, quiero aclarar que los datos empleados en esta entrada son totalmente inventados por mí y no corresponden a ningún experimento real. Los he generado con un ordenador con el fin de explicar el ejemplo, así que no quiero que ningún vendedor de tensiómetros de muñeca me venga con reclamaciones.

Para finalizar, deciros que este método se usa solo cuando se quiere valorar el grado de acuerdo entre variables cuantitativas. Existen otros métodos, como el índice kappa de concordancia, para cuando tratamos con resultados cualitativos. Pero esa es otra historia…