
Manuel Molina Arias
Servicio de Gastroenterología
Hospital Infantil Universitario La Paz. Madrid
No me negaréis que es un nombre bastante curioso para un gráfico. Al pensar en el nombre a uno se le viene a la cabeza una imagen de una caja de zapatos con bigotes de gato, pero, en realidad, yo creo que este gráfico se parece más a las naves de caza de tipo tie fighter de la Guerra de las Galaxias. En cualquier caso, el gráfico de caja y bigotes, cuyo nombre formal es el de gráfico de caja (boxplot en inglés), es empleado con muchísima frecuencia en estadística por sus interesantes capacidades descriptivas.
Para saber de qué hablamos, tenéis representados dos gráficos de caja en la Figura 1. Como veis, el gráfico, que puede representarse en vertical y en horizontal, consta de una caja y dos segmentos (los bigotes).
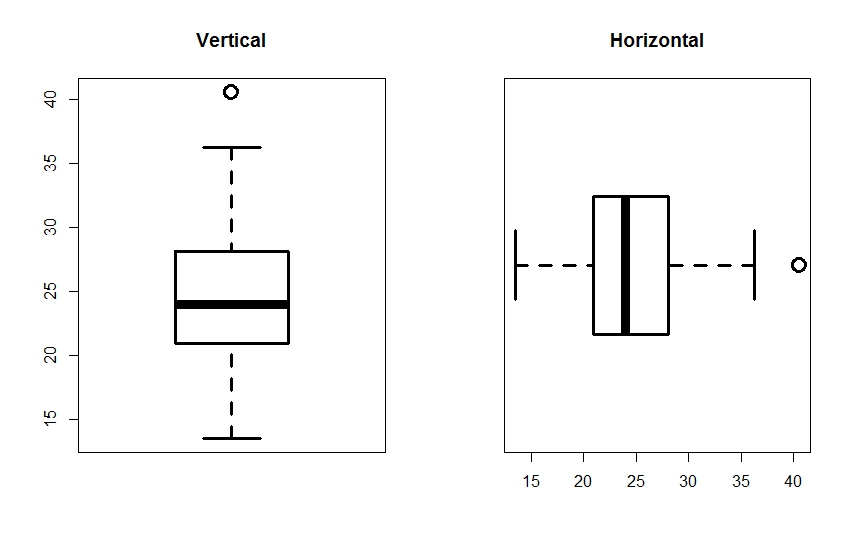
Vamos ahora con los bigotes. El superior se extiende hasta el valor máximo de la distribución, pero no puede llegar más allá de 1,5 veces el rango intercuartílico. Si existen valores más altos que la mediana más 1,5 veces el rango intercuartílico, éstos se representan como puntos más allá del extremo del bigote superior. Estos puntos son los denominados valores extremos, outliers en inglés. Vemos en nuestro ejemplo que hay un outlier que se sitúa más allá del bigote superior. Si no hay valores extremos u outliers, el máximo de la distribución lo marca el extremo del bigote superior. Si los hay, el máximo será el valor extremo más alejado de la caja.
Por añadidura, todo esto vale para el bigote inferior, que se extiende hasta el valor mínimo cuando no hay valores extremos o hasta la mediana menos 1,5 veces el rango intercuartílico cuando los haya. En estos casos, el valor mínimo será el outlier más alejado de la caja por debajo del bigote inferior.
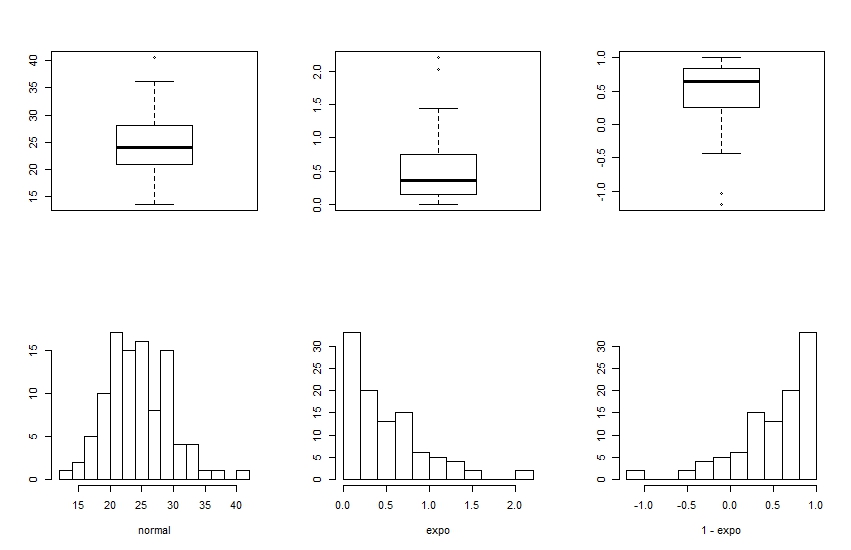
Pues ya podemos comprender la utilidad del gráfico de caja. De un vistazo podemos obtener la mediana y el rango intercuartílico de su distribución e intuir la simetría de la distribución. Es fácil imaginarse cómo es el histograma de una distribución viendo su gráfico de caja, como podéis ver en la Figura 2. El primer gráfico corresponde a una distribución simétrica, próxima a la normal, ya que la mediana está centrada en la caja y los dos bigotes son más o menos simétricos.
Si nos fijamos en la distribución central, la mediana está desplazada hacia el borde inferior de la caja y el bigote superior es más largo que el inferior. Esto es así porque la distribución tiene la mayoría de los datos hacia la izquierda y una larga cola hacia la derecha, como puede verse en su histograma. Lo mismo que hemos dicho para la distribución central vale para la tercera, pero en este caso el bigote largo es el inferior y el sesgo es hacia la izquierda.
Por último, este tipo de gráfico sirve también para comparar varias distribuciones. En la figura 3 podéis ver dos distribuciones aparentemente normales y con medianas muy similares. Si queremos hacer un contraste de hipótesis sobre la igualdad de sus medias, primero tenemos que saber si sus varianzas son iguales (si existe homocedasticidad) para saber qué tipo de test hay que utilizar.

Y esto es todo lo que quería contar sobre esta caja con bigotes, que tan útil resulta en estadística descriptiva. Ni que decir tiene que, aunque nos sirve para saber aproximadamente si la distribución se ajusta a una normal o si las varianzas de varias distribuciones son semejantes, existen pruebas específicas para estudiar estos puntos de forma matemática. Pero esa es otra historia…
Lectura recomendada
Martínez Gonzaléz MA, Gea A, Sayón-Orea C. Procedimientos descriptivos. En: Martínez González MA, Sánchez-Villegas A, Toledo Atucha EA, Faulin Fajardo J, eds. Bioestadística amigables, 3ª ed. Elsevier España SA. Barceloma, 2014; pg: 13-64. (web)




Excelente la explicación y tiene razón se parece las naves de la guerra de las galaxias
Saludos