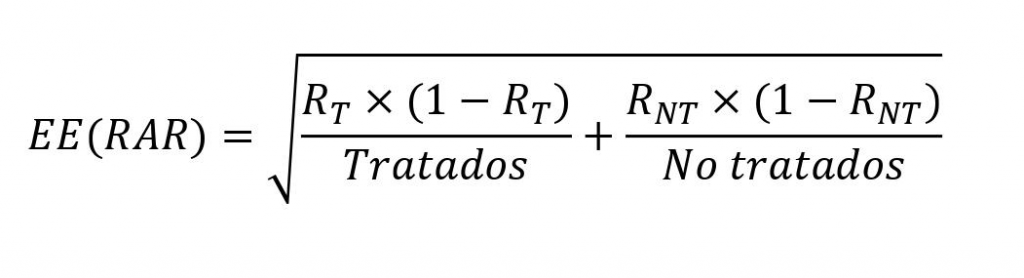Manuel Molina Arias
Servicio de Gastroenterología. Hospital Infantil Universitario La Paz. Madrid.
El número necesario a tratar (NNT) es una medida de impacto que nos informa de forma sencilla sobre la eficacia de una intervención o sobre sus efectos secundarios. Si el tratamiento intenta evitar eventos desagradables, el NNT nos mostrará una apreciación de los pacientes que tenemos que someter al tratamiento para evitar uno de esos eventos. En este caso hablamos de NNTB, o número a tratar para beneficiar.
En otros casos, la intervención puede producir efectos adversos. Entonces hablaremos del NNTD o número a tratar para dañar a uno (producir un evento desagradable).
El cálculo del NNT es sencillo cuando disponemos de una tabla de contingencia como la que vemos en la figura 1. Habitualmente se calcula como el inverso de la reducción absoluta del riesgo (1/RAR) y se proporciona como un valor fijo. El problema es que esto ignora el carácter probabilístico del NNT, por lo que los más correcto sería especificar su intervalo de confianza al 95% (IC95), como hacemos con el resto de las medidas.

Ya sabemos que el IC95 de cualquier medida responde a la fórmula siguiente:
IC95(X) = X ± (1,96 x EE(X)), donde EE es el error estándar.
Con lo que los límites inferior y superior del intervalo serían los siguientes:
X – 1,96 EE(X), X + 1,96 EE(X)
Y aquí nos surge un problema con el IC95 del NNT. Este intervalo no puede calcularse directamente porque el NNT no tiene una distribución normal. Por ello, se han inventado algunas argucias para calcularlo, como calcular el IC95 de la RAR y utilizar sus límites para calcular los del NNT, según vemos a continuación:
IC95 (RAR) = RAR – 1,96(EE (RAR)), RAR + 1,96(EE (RAR))
IC (NNT) = 1 / límite superior del IC95 (RAR), 1 / límite inferior del IC95 (RAR) (ponemos en límite superior del RAR para calcular el inferior del NNT, y viceversa, porque al ser el tratamiento beneficioso la reducción del riesgo sería en rigor un valor negativo [RT – RNT], aunque habitualmente hablamos de él en valor absoluto).
Ya sólo necesitamos saber cómo calcular el EE de la RAR, que resulta que se hace con una fórmula un poco antipática que os pongo solo por si alguno tiene curiosidad de verla:
En la figura 2 podéis ver un ejemplo numérico para calcular el NNT y su intervalo. Veis que el NNT = 25, con un IC95 de 15 a 71. Fijaos en la asimetría del intervalo ya que, como ya hemos dicho, no sigue una distribución normal. Además, lejos del valor fijo de 25, los valores del intervalo dicen que en el mejor de los casos tendremos que tratar a 15 pacientes para evitar un efecto adverso, pero en el peor de los casos este valor puede ascender hasta 71.

A toda la dificultad anterior para su cálculo, surge otra dificultad añadida cuando el IC95 de la RAR incluye el cero. En general, cuanto menor sea el efecto del tratamiento (menor RAR) mayor será el NNT (habrá que tratar a más para conseguir evitar un evento desagradable), por lo que en el valor extremo de que el efecto sea cero, el NNT valdrá infinito (habría que tratar infinitos pacientes para evitar un evento desagradable).
Así que es fácil imaginar que si el IC95 de la RAR incluye el cero, el IC95 del NNT incluirá el infinito. Será un intervalo discontinuo con un límite de valor negativo y otro positivo, lo que puede plantear problemas para su interpretación.
Por ejemplo, supongamos que tenemos un ensayo en el que calculamos una RAR de 0,01 con un IC95 de -0,01 a 0,03. Con el valor fijo no tenemos problemas, el NNT es de 100 pero, ¿qué pasa con el intervalo? Pues que iría de -100 a 33, pasando por el infinito (en realidad, de menos infinito a -100 y de 33 a infinito).
¿Cómo interpretamos un NNT negativo? En este caso, como ya dijimos, estamos tratando con un NNTB, por lo que su valor negativo lo podemos interpretar como un valor positivo de su alter ego, el NNTD. En nuestro ejemplo, -100 querría decir que provocaremos un efecto adverso por cada 100 tratados. En resumen, que nuestro intervalo nos diría que podríamos producir un evento por cada 100 tratados, en el peor de los casos, o evitar uno por cada 33 tratados, en el mejor de los casos. Esto consigue que el intervalo sea continuo y que incluya la estimación puntual, pero tendrá poca aplicación como medida práctica. En el fondo, quizás tenga poco sentido calcular el NNT cuando la RAR no sea significativa (su IC95 incluya el cero).
Llegados a estas alturas, la cabeza empieza a echarnos humo, así que vamos a ir terminando por hoy. Ni que decir tiene que todo lo que he explicado sobre el cálculo del intervalo puede hacerse a golpe de clic con cualquiera de las calculadoras disponibles en Internet, con lo que no tendremos que hacer ninguna operación matemática.
Además, aunque el cálculo del NNT resulta sencillo cuando disponemos de una tabla de contingencia, en muchas ocasiones de lo que disponemos es de valores ajustados de riesgos obtenidos de modelos de regresión. Entonces, la matemática para el cálculo del NNT y su intervalo se complica un poco. Pero esa es otra historia…
BIBLIOGRAFÍA
Gómez-Acebo I, Dierssen-Sotos T, Llorca J. Número necesario de tratamientos: interpretación y estimación en análisis multivariables y con datos censurados. Med Clin (Barc):2014;142:451-6.
(HTML + PDF)