Manuel Molina Arias.
Servicio de Gastroenterología.
Hospital Infantil Universitario La Paz.
Madrid. España.
Cómo citar este artículo: Molina, M. (2022). Paso a paso. Prueba de la t de Student para muestras independientes. Revista Electrónica AnestesiaR, 14(8). https://doi.org/10.30445/rear.v14i8.1060
Ya vimos en una entrada anterior cómo William Sealy Gosset, con la ayuda de algunos amigos, diseñó una distribución de probabilidad para poder llevar a cabo su noble empeño de mejorar la producción de las destilerías Guinness.
Esta distribución se publicó bajo pseudónimo, por lo que es conocida como distribución de la t de Student, en lugar de t de Gosset, o algo parecido.
La distribución de probabilidad de la t de Student permite comparar dos medias cuando las muestras son pequeñas y se desconoce la varianza poblacional, situación que es bastante frecuente.
Así que, sirviéndonos de una historia que es fruto de mi imaginación (aunque bien podría ser cierta), vamos a ver cómo Gosset sacaba partido de esta nueva distribución.
Unos preparativos previos
Vamos a suponer que en la granja de la factoría se ha venido utilizando hasta ahora un fertilizante, al que llamaremos A para no esforzarnos mucho, pero que han hecho algunos experimentos con uno nuevo, al que llamaremos B.
El fertilizante B consigue aumentar la producción de malta, pero Gosset cree que la cerveza elaborada con esta malta es un poco más ácida, lo que, de ser cierto, lo descartaría como sustituto del clásico fertilizante A.
Para salir de dudas, Gosset decide dividir una sección del terreno de la granja en 50 parcelas diferentes, sembrando cada una de ellas y utilizando, de forma aleatoria, el fertilizante A en 25 de las parcelas y el B en las otras 25.
Una vez obtenidos los cultivos, elabora la cerveza y mide el pH de cada una de las 50 muestras. El resultado obtenido podéis descargarlo de este enlace .
Ahora que ya tenemos los datos, vamos a ver si la impresión de Gosset es correcta.
Paso 1. Análisis descriptivo de los datos
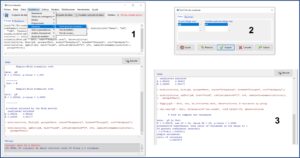
Lanzamos el programa R y abrimos RCommander con el comando library(Rcmdr).
El fichero que hemos descargado está en formato Excel, así que seleccionamos la opción del menú Datos->Importar datos->desde un archivo Excel… En la ventana emergente ponemos un nombre (por ejemplo, cultivos), seleccionamos la primera y tercera opciones y pulsamos “Aceptar”. Con esto ya tenemos el conjunto de datos activo, que es “cultivos” (si no es así, seleccionadlo).
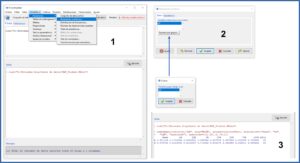
Ya que tenemos cargados los datos, veamos cuáles son los pHs de las dos muestras. Seleccionamos el menú Estadísticos->Resúmenes->Resúmenes numéricos. En la ventana emergente seleccionamos la variable “pH” (la única cuantitativa que hay es este conjunto de datos) y clicamos en el botón “Resumir por grupos…” para seleccionar la variable “fert” (el tipo de fertilizante).
Si no hacemos la selección por grupos, R nos mostrará el análisis de las 50 muestras en conjunto, pero nosotros estamos interesados en ver los pH de las muestras de los dos fertilizantes por separado. Todo esto podéis verlo en la figura 1.
Si os fijáis en la ventana de salida (3), R proporciona el tamaño muestral, la media, la desviación estándar, el recorrido o rango intercuartílico (IQR), los valores máximo y mínimo (100% y 0%), la mediana (50%) y los cuartiles (25% y 75%).
Efectivamente, la media de pH del grupo A es de 4,40 y la del grupo B de 4.07. Parece que, efectivamente, la cerveza obtenida con el fertilizante B es más ácida, al menos en nuestra muestra. Sin embargo, esta diferencia puede deberse al azar, ya que estamos utilizando una muestra pequeña y hay cierta dispersión de los datos (de 0,17 y 0,21 unidades de pH en los grupos A y B, respectivamente).
Cabe la posibilidad de que, si repitiésemos el experimento, el resultado fuese distinto.
Pues bien, para medir la probabilidad de que la diferencia que observamos se deba a la casualidad, emplearemos la prueba de la t de Student.
Paso 2. Comprobar la normalidad de los datos
La prueba de la t de Student compara las medias de una variable continua clasificada según las dos categorías de una variable nominal dicotómica. Estos dos grupos pueden ser independientes (cada sujeto puede pertenecer solamente a una de las dos categorías) o tratarse de muestras apareadas.
En nuestro caso, utilizaremos la prueba de la t de Student para muestras independientes, una vez que comprobemos que se cumplen dos supuestos:
1. La variable continua sigue una distribución normal para las dos categorías de la variable nominal.
2. Existe homocedasticidad, lo que quiere decir que la varianza de los valores de la variable continua es la misma en los dos grupos de la variable nominal dicotómica.
Comprobemos en primer lugar si se cumple el supuesto de normalidad.
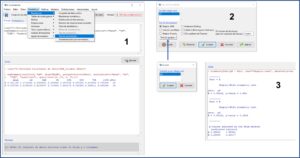
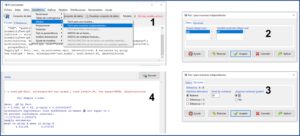
Seleccionamos el menú Estadísticos->Resúmenes->Test de normalidad… En la ventana emergente seleccionamos la variable “pH” (la única cuantitativa que hay es este conjunto de datos), marcamos la prueba que queramos (por ejemplo, Shapiro-Wilk) y clicamos en el botón “Test por grupos…” para seleccionar la variable “fert” (el tipo de fertilizante). Finalmente, pulsamos en aceptar y obtenemos el resultado en la ventana de salida (figura 2).
Los valores del estadístico W para los fertilizantes A y B son de 0,98 y 0,95, respectivamente, con un valor de significación estadística de p = 0,95 para el grupo A y p = 0,29 para el grupo B. Como p > 0,05 en los dos grupos, no podemos rechazar la hipótesis nula que, para la prueba de Shapiro-Wilk, supone que los datos siguen una distribución normal.
Sin embargo, ya sabemos que las pruebas numéricas para comprobar la normalidad son poco potentes, sobre todo si la muestra es pequeña, por lo que se aconseja comprobar su resultado con algún método gráfico.
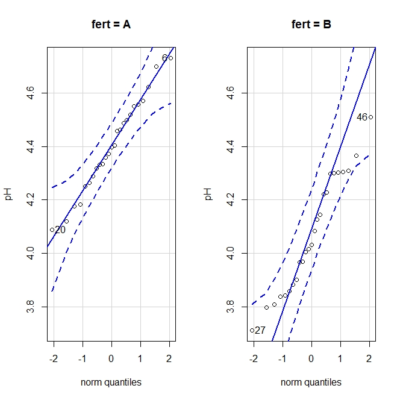
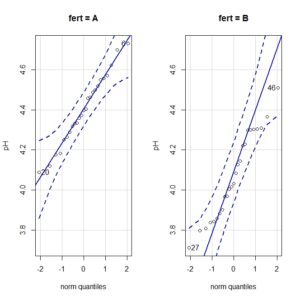
Vamos a realizar los gráficos de comparación de cuantiles. Para obtenerlos, seleccionamos el menú Gráficas->Gráfica de comparación de cuantiles… y, en la ventana emergente, clicamos el botón “Gráfica por grupos” para obtener los gráficos para cada fertilizante, que podéis ver en la figura 3.
Los gráficos de comparación de cuantiles comparan los valores de los cuantiles de la distribución con los que deberían tener si los datos siguiesen una distribución normal. Si esto es así, los valores se alinean a lo largo de la diagonal del gráfico. Viendo los gráficos, podemos asumir la normalidad de los datos (aunque hay cierta desviación en el caso de los valores del grupo B).
Paso 3. Comprobar el supuesto de homocedasticidad
Sabemos que el cociente de dos varianzas sigue una distribución de probabilidad de la F de Snedecor.
En el caso de existir homocedasticidad, el valor de este cociente debe estar próximo a la unidad. Cuánto más se separe de la unidad, mayor será la probabilidad de que las varianzas sean realmente diferentes y que la diferencia observada no se deba al azar.
Para calcular esta probabilidad, podemos realizar la prueba de la F de Snedecor, que tiene en cuenta los grados de libertad de numerador y denominador del cociente de varianzas.
Seleccionamos el menú Estadísticos->Varianzas->Test F para dos varianzas… En este caso tan sencillo, solo tenemos que pulsar “Aceptar” en la ventana emergente y R nos mostrará los resultados en la ventana de salida (figura 4).
Podemos ver de varias maneras que, en efecto, se cumple el supuesto de homocedasticidad.
En primer lugar, el valor del estadístico F = 0,63, con una p = 0,26, por lo que no podemos rechazar la hipótesis nula que, para esta prueba, asume que las dos varianzas son iguales.
Además, si os fijáis en la parte final de los resultados, el cociente de varianzas vale 0,63, con un intervalo de confianza del 95% de 0,27 a 1,43. Como el intervalo incluye el valor nulo (la unidad), podemos decir que la diferencia observada entre las dos varianzas no es estadísticamente significativa.
Paso 4. Realizamos la prueba de la t de Student
Ya solo nos queda realizar el contraste de hipótesis, utilizando para ello la prueba de la t de Student para muestras independientes. En este contraste se asume la hipótesis nula de igualdad de medias (la diferencia observada se debe al azar).
Seleccionamos el menú Estadísticos->Medias->Test t para muestras independientes… (figura 5). Nos aparecerá una ventana (2), en la que las variables ya están seleccionadas, y pulsaremos en la pestaña “Opciones” (3) para marcar que queremos un contraste bilateral y que asumimos la igualdad de varianzas. Aceptamos todo y R nos proporciona el resultado en la ventana de salida.
Podemos ver que t = 5,95, con un valor de p muy inferior a 0,05, con lo que podemos descartar la hipótesis nula de igualdad de medias y asumir que las diferencias observadas se deben al fertilizante utilizado. En otras palabras: Gosset tenía razón y con el fertilizante B se obtiene una cerveza más ácida.
Nos vamos…
En esta entrada hemos visto como comparar dos medias independientes cuando la muestra es pequeña, siempre que se cumplan los supuestos de normalidad y homocedasticidad. Pero ¿qué podemos hacer si estos supuestos no se cumplen? En estos casos tenemos tres opciones.
La primera, utilizar la prueba de la t de Student si la muestra es grande y la desviación es ligera. Si la muestra no es muy pequeña, la t de Student es bastante robusta ante el incumplimiento de estos supuestos, sobre todo el de normalidad.
La segunda, podemos intentar transformar los datos y ver si los datos transformados sí siguen la distribución normal.
La tercera, quizás la más aconsejable, utilizar el equivalente no paramétrico de la prueba de la t de Student, que no es otro que la prueba de la U de Mann-Whitney. Pero esa es otra historia…
Bibliografía
– Student. The probable error of a mean. Biometrika.1908;6:1-25. (https://www.york.ac.uk/depts/maths/histstat/student.pdf)
– Toledo E, López del Burgo C, Sayón-Orea C, Martínez-González MA. Comparación de medias entre dos grupos. En: Martínez-Sánchez MA, Sánchez-Villegas A, Toledo EA, Faulin J, eds. Bioestadística amigable, 3ª ed. Elsevier España, SL. Madrid, 2014; 175-99. (HTML)